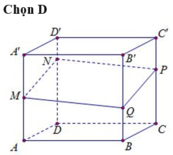
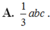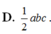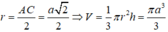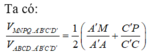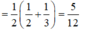Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
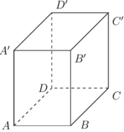
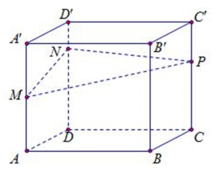
Ta đặt AB=x, AD=y, AA'=z. Khi đó theo giả thiết ta có:
x y = 2 a 2 x z = 3 a 2 y z = 6 a 2 ⇔ x y = 2 a 2 x z = 3 a 2 y z = 6 a 2 x y z = 6 a 3 ⇔ x = a y = 2 a z = 3 a
Vậy thể tích khối hôp chữ nhật V=6a3.

Phương pháp:
Công thức tính thể tích khối hộp chữ nhật ABCD.A'B'C'D' là V = AA'.AB.AD
Cách giải:
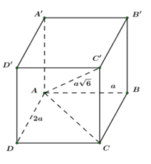
Ta có: ![]() (định lý Pitago)
(định lý Pitago)
Xét tam giác ACC’ vuông tại C ta có:
![]()
![]()
![]()
Chọn C.