Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì π < a < 3 π 2 nên sina < 0; cosa < 0. Ta có
sin α - 2 cos α = 1 sin 2 α + cos 2 α = 1 ⇒ 1 + 2 cos α 2 + cos 2 α = 1 ⇒ 5 cos 2 α + 4 cos α = 0 ⇒ cos α = - 4 5
Suy ra α = - 1 - cos 2 α = - 3 5 ; tan α = 3 4 ; c o t α = 4 3 . Vậy A = 2tana - cota = 2 . 3 4 - 4 3 = 1 6
Đáp án B

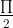 < a < π => sina > 0, cosa < 0
< a < π => sina > 0, cosa < 0
cos2a = 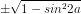 = ±
= ±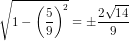
Nếu cos2a = 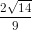 thì
thì
sina = 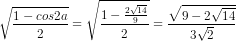
= 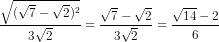
cosa = -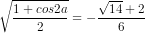
Nếu cos2a = -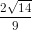 thì
thì
sina = 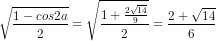
cosa = -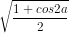
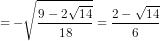

Đáp án C
Phương pháp:
- Xác định góc giữa hai đường thẳng: Cho a, b là hai đường thẳng bất kì, đường thẳng a’ // a => (a;b) = (a’;b)
Cách giải:

Gọi O, M lần lượt là tâm của hình chữ nhật ABCD và trung điểm của SA
=> MO là đường trung bình của tam giác SAC
=>MO//SC
=>(BD,SC)=(BD,MO)
+) ABCD là hình chữ nhật
![]()
![]()
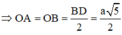
+) M là trung điểm SA
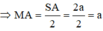
Tam giác MAB vuông tại A
![]()
Tam giác MAO vuông tại A
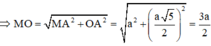
+) Xét tam giác MBO:
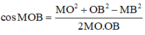

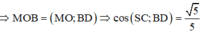

∫ 0 a cos x + a 2 d x = ∫ 0 a cos x + a 2 d x + a 2 = sin x + a 2 0 4 = sin a + a 2 - sin a 2
Với a = 2 π ta có sin 2 π + 2 π = sin 2 π
Đáp án D
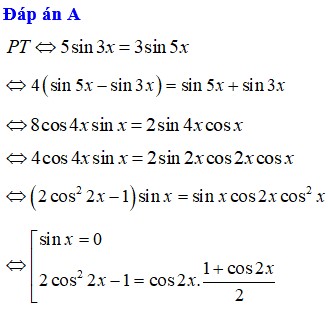
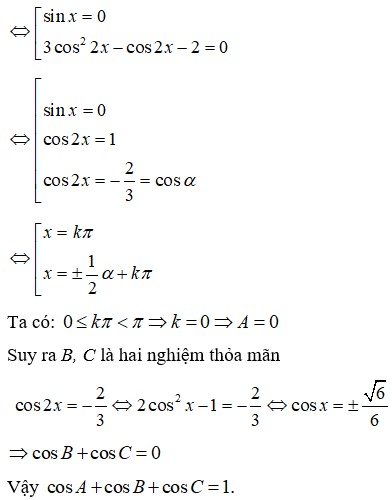
 và
và 
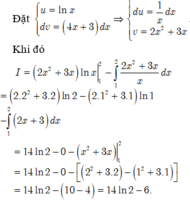
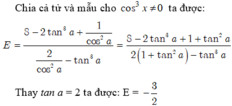
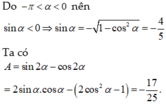
a) π < a <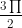 => sina < 0, cosa < 0, tana > 0
=> sina < 0, cosa < 0, tana > 0
sin2a = 2sinacosa = 2(-0,6)(-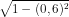 ) = 0,96
) = 0,96
cos2a = cos2 a – sin2 a = 1 – 2sin2 a = 1 - 0,72 = 0,28
tan2a =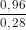 ≈ 3,1286
≈ 3,1286
b)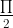 < a < π => sina > 0, cosa < 0
< a < π => sina > 0, cosa < 0
sina =
sin2a = 2sinacosa = 2.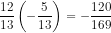
cos2a = 2cos2a - 1 = 2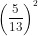 - 1 = -
- 1 = -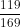
tan2a =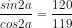
c)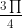 < a < π =>
< a < π => 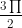 < 2a < 2π => sin2a < 0, cos2a > 0, tan2a < 0
< 2a < 2π => sin2a < 0, cos2a > 0, tan2a < 0
sin2a = - 1 = -0,75
- 1 = -0,75
cos2a =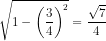
tan2a = -