Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P=\dfrac{1}{49}+\dfrac{2}{48}+\dfrac{3}{47}+...+\dfrac{48}{2}+\dfrac{49}{1}\)
\(P=\left(\dfrac{1}{49}+1\right)+\left(\dfrac{2}{48}+1\right)+\left(\dfrac{3}{47}+1\right)+...+\left(\dfrac{48}{2}+1\right)+1\)
\(P=\dfrac{50}{49}+\dfrac{50}{48}+\dfrac{50}{47}+...+\dfrac{50}{2}+\dfrac{50}{50}\)
\(P=50\left(\dfrac{1}{2}+...+\dfrac{1}{49}+\dfrac{1}{50}\right)\)
\(\dfrac{S}{P}=\dfrac{\dfrac{1}{2}+...+\dfrac{1}{49}+\dfrac{1}{50}}{50\left(\dfrac{1}{2}+...+\dfrac{1}{49}+\dfrac{1}{50}\right)}=\dfrac{1}{50}\)

Ta có: \(P=\dfrac{1}{49}+\dfrac{2}{48}+\dfrac{3}{47}+...+\dfrac{48}{2}+\dfrac{49}{1}\)
\(P=\left(1+\dfrac{1}{49}\right)+\left(1+\dfrac{2}{48}\right)+\left(1+\dfrac{3}{47}\right)+...+\left(1+\dfrac{48}{2}\right)+1\)
\(P=\dfrac{50}{49}+\dfrac{50}{48}+\dfrac{50}{47}+...+\dfrac{50}{2}+\dfrac{50}{50}\)
\(P=50\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{50}\right)\)
\(\Rightarrow\)\(\dfrac{S}{P}=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{50}}{50\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{50}\right)}\)\(=\dfrac{1}{50}\)

P = 1/49+2/48+3/47+...+48/2+49/1
Cộng 1 váo mỗi p/s trong 48 p/s đầu , trừ p/s cuối đi 48 ta được
P=(1/49+1)+(2/48+1)+...+(48/2+1)+1
P= 50/49+50/48+....+50/2+50/50
Đưa ps cuối lên đầu
P=50/50+50/49+50/48+...+50/2
=50.(1/50+1/49+1/48+...+1/4+1/3+1/2)
=50S
=> S/P=1/50

Lời giải:
Gọi tử số là $T$
\(T=(1-\frac{1}{6})+(1-\frac{2}{7})+(1-\frac{3}{8})+....+(1-\frac{88}{93})\)
\(=\frac{5}{6}+\frac{5}{7}+\frac{5}{8}+....+\frac{5}{93}=5(\frac{1}{6}+\frac{1}{7}+...+\frac{1}{93})\)
Gọi mẫu số là $M$
\(M=\frac{-1}{2}(\frac{1}{6}+\frac{1}{7}+....+\frac{1}{93})\)
Do đó:
\(C=\frac{5(\frac{1}{6}+\frac{1}{7}+...+\frac{1}{93})}{\frac{-1}{2}(\frac{1}{6}+\frac{1}{7}+...+\frac{1}{93})}=\frac{5}{\frac{-1}{2}}=-10\)

Ta có:
P= \(\dfrac{1}{49}+\dfrac{2}{48}+...+\dfrac{48}{2}+\dfrac{49}{1}\)
P= \(\dfrac{1}{49}+\dfrac{2}{48}+...+\dfrac{48}{2}+\left(1+1+...+1\right)\)(có 49 chữ số 1)
P= \(\left(\dfrac{1}{49}+1\right)+\left(\dfrac{2}{48}+1\right)+...+\left(\dfrac{48}{2}+1\right)+1\)
P= \(\dfrac{50}{49}+\dfrac{50}{48}+...+\dfrac{50}{2}+\dfrac{50}{50}\)
P= \(50.\left(\dfrac{1}{50}+\dfrac{1}{49}+...+\dfrac{1}{2}\right)\)
⇒ \(\dfrac{S}{P}=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{50}}{50.\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{50}\right)}\)
⇒ \(\dfrac{S}{P}=\dfrac{1}{50}\)
Vậy \(\dfrac{S}{P}=\dfrac{1}{50}\)

a: 51/56=1-5/56
61/66=1-5/66
mà -5/56<-5/66
nên 51/56<61/66
b: 41/43<1<172/165
c: \(\dfrac{101}{506}>0>-\dfrac{707}{3534}\)

a: \(=\dfrac{14-2+9}{32}\cdot\dfrac{4}{5}=\dfrac{21}{5}\cdot\dfrac{1}{8}=\dfrac{21}{40}\)
b: \(=10+\dfrac{2}{9}+2+\dfrac{3}{5}+6+\dfrac{2}{9}=18+\dfrac{47}{45}=\dfrac{857}{45}\)
c: \(=\dfrac{3}{10}-\dfrac{12}{5}+\dfrac{1}{10}=\dfrac{4}{10}-\dfrac{12}{5}=\dfrac{2}{5}-\dfrac{12}{5}=-2\)
d: \(=\dfrac{-25}{30}\left(\dfrac{37}{44}+\dfrac{13}{44}-\dfrac{6}{44}\right)=\dfrac{-25}{30}\cdot1=-\dfrac{5}{6}\)
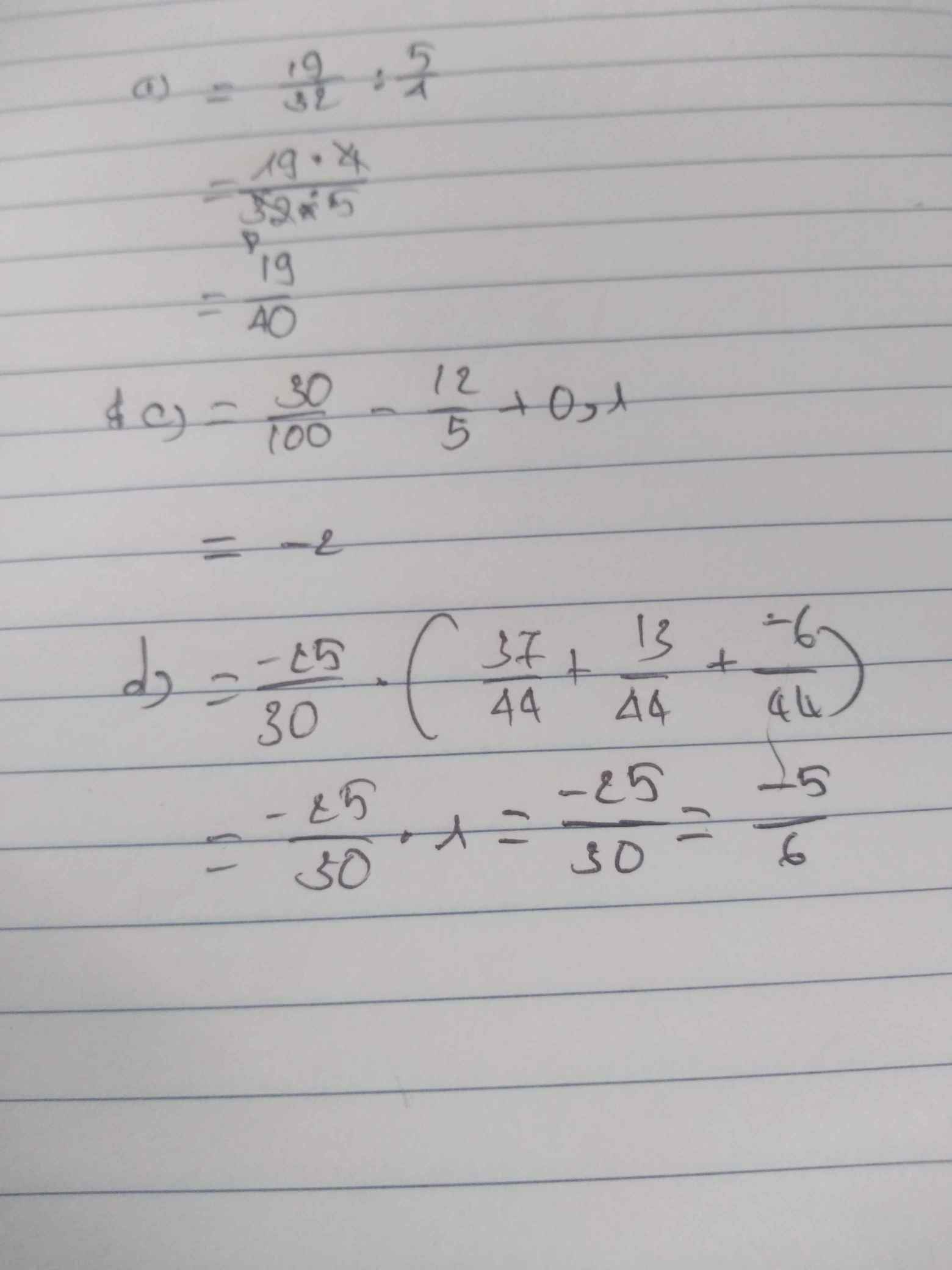
\(S=\dfrac{1}{30}+\dfrac{2}{48}+\dfrac{3}{88}+\dfrac{4}{165}+\dfrac{5}{300}\\ S=\dfrac{1}{5.6}+\dfrac{2}{6.8}+\dfrac{3}{8.11}+\dfrac{4}{11.15}+\dfrac{5}{15.20}\\ S=\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{15}+\dfrac{1}{15}-\dfrac{1}{20}\\ S=\dfrac{1}{5}-\dfrac{1}{20}\\ S=\dfrac{4}{20}-\dfrac{1}{20}\\ S=\dfrac{3}{20}\)