Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x^6-y^6\)
\(=\left(x^3-y^3\right)\left(x^3+y^3\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)\left(x+y\right)\left(x^2-xy+y^2\right)\)
hk
tốt

(3x-1)^2 - 16 = (3x-1)^2 - 4^2
= (3x-1-4)(3x-1+4)
= (3x-5)(3x+3)
\(\left(3x-1\right)^2-16\)
\(=\left(3x-1\right)^2-4^2\)
\(=\left(3x-1-4\right)\left(3x-1+4\right)\)
\(=\left(3x-5\right)\left(3x+3\right)\)
\(=3\left(x+1\right)\left(3x-5\right)\)

a. Ta có : (x + y)[(x - y)2 + xy]
= (x + y)(x2 - 2xy + y2 + xy)
= (x + y)(x2 - xy + y2)
= x3 + y3
b. Ta có : x3 + y3 - xy(x + y)
= x3 + y3 - x2y - xy2
=x2(x - y) + y2(y - x)
= (x - y)(x2 - y2)
= (x - y)2.(x + y) đpcm
c) Ta có (x + y)3 - 3xy(x + y)
= (x + y)[(x + y)2 - 3xy)
= (x + y)(x2 + 2xy + y2 - 3xy)
= (x + y)(x2 - xy + y2) (đpcm)
a) VP = ( x + y )( x2 - 2xy + y2 + xy ) = ( x + y )( x2 - xy + y2 ) = x3 + y3 = VT ( đpcm )
b) VP = ( x + y )( x - y )2 = ( x + y )( x2 - 2xy + y2 ) = x3 - 2x2y + xy2 + x2y - 2xy2 + y3 = x3 + y3 - x2y - xy2 = x3 + y3 - xy( x + y ) = VT ( đpcm )
c) VP = x3 + 3x2y + 3xy2 + y3 - 3x2y - 3xy2 = x3 + y3 = ( x + y )( x2 - xy + y2 ) = VT ( đpcm )


- \(A=4x-x^2+3=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\)
Dấu "=" xảy ra khi và chỉ khi x = 2
Vậy Max A = 7 <=> x = 2
- \(B=2x^2-6x=2\left(x^2-3x\right)=2\left(x^2-2.x.\frac{3}{2}+\frac{9}{4}\right)-\frac{9}{2}=2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}\ge-\frac{9}{2}\)
Dấu "=" xảy ra khi và chỉ khi x = \(\frac{3}{2}\)
Vậy Min B = \(-\frac{9}{2}\Leftrightarrow x=\frac{3}{2}\)
- \(C=-3x^2+x=-3\left(x^2-\frac{1}{3}x\right)=-3\left(x^2-2.x.\frac{1}{6}+\frac{1}{36}\right)+\frac{1}{12}=-3\left(x-\frac{1}{6}\right)^2+\frac{1}{12}\le\frac{1}{12}\)Dấu "=" xảy ra khi và chỉ khi x = \(\frac{1}{6}\)
Vậy Max C = \(\frac{1}{12}\Leftrightarrow x=\frac{1}{6}\)
Bạn có thể giải rõ ra cho mình đc ko, mình ko hiểu bước thứ 2 của các câu trên
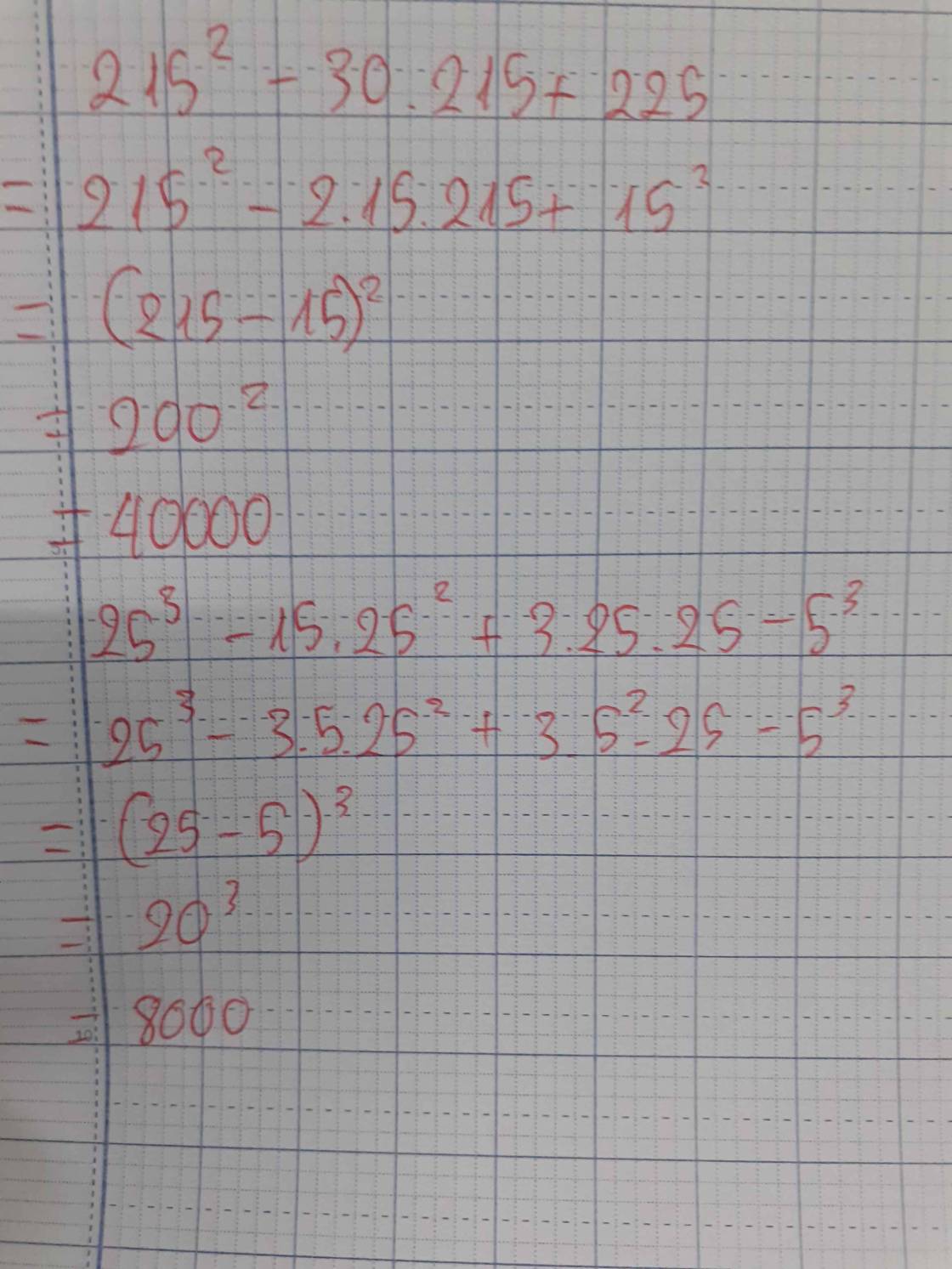
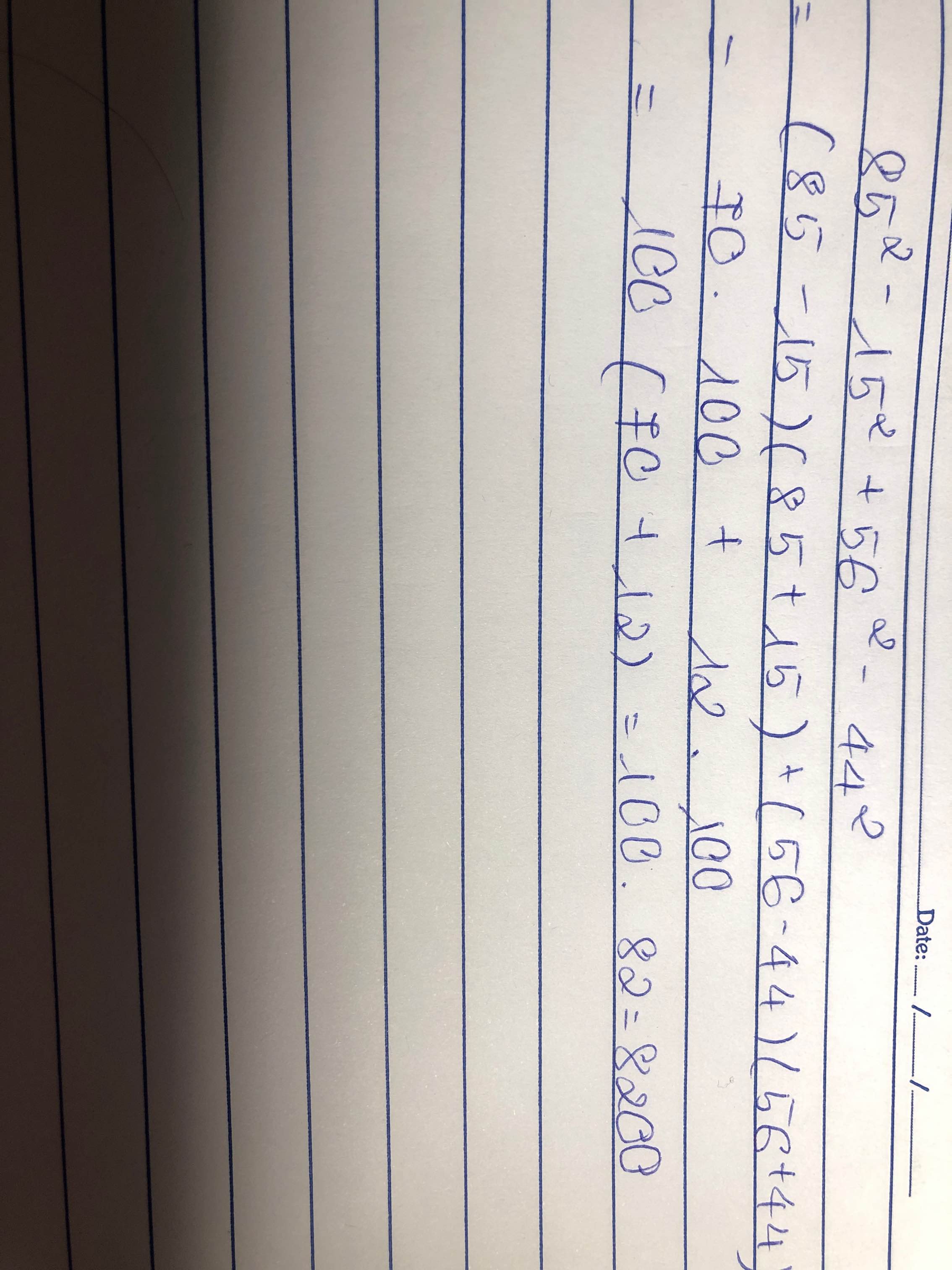

\(299.301=\left(300-1\right)\left(300+1\right)=300^2-1^2=90000-1=89999\)
\(299\cdot301=300^2-1=89999\)