Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: D\(=\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{4}\right)...\left(1-\dfrac{1}{2005}\right)\)
\(\Leftrightarrow D=\dfrac{1}{2}.\dfrac{2}{3}.\dfrac{3}{4}...\dfrac{2004}{2005}=\dfrac{1.2.3...2004}{2.3.4...2005}=\dfrac{1}{2005}\)
Ta có: \(E=\dfrac{1^2}{1.3}.\dfrac{2^2}{2.4}.\dfrac{3^2}{3.5}...\dfrac{999^2}{999.1000}.\dfrac{1000^2}{1000.1001}=\dfrac{\left(1.2.3.4...1000\right)\left(1.2.3.4...1000\right)}{\left(1.2.3....1000\right)\left(3.4.5....1001\right)}=\dfrac{2}{1001}\)

Ta có \(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}=\dfrac{1}{6}-\dfrac{1}{6}=0\) nên Q = 0.

A = ( \(\dfrac{1}{2}\) + 1)(\(\dfrac{1}{3}\) + 1).(\(\dfrac{1}{4}\) + 1)....(\(\dfrac{1}{999}\) + 1)
A = \(\dfrac{3}{2}\).\(\dfrac{4}{3}\).\(\dfrac{5}{4}\).......\(\dfrac{1000}{999}\)
A = \(\dfrac{3.4.5......999}{3.4.5......999}\). \(\dfrac{1000}{2}\)
A = 1 \(\times\) 500
A = 500

\(B=\left(1-\dfrac{1}{2}\right)\left(1+\dfrac{1}{2}\right)\cdot\left(1-\dfrac{1}{3}\right)\left(1+\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{100}\right)\left(1+\dfrac{1}{100}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot...\cdot\dfrac{99}{100}\cdot\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{101}{100}\)
\(=\dfrac{1}{100}\cdot\dfrac{101}{2}=\dfrac{101}{200}\)

1. \(\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right).\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)\)
\(=\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right).0\)
\(=0\)

\(Q=\left(\dfrac{1}{99}+\dfrac{12}{999}+\dfrac{123}{9999}\right)\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)\)
\(Q=\left(\dfrac{1}{99}+\dfrac{12}{999}+\dfrac{123}{9999}\right)\left(\dfrac{3}{6}-\dfrac{2}{6}-\dfrac{1}{6}\right)\)
\(Q=\left(\dfrac{1}{99}+\dfrac{12}{999}+\dfrac{123}{9999}\right)\cdot\dfrac{0}{6}\)
\(Q=\left(\dfrac{1}{99}+\dfrac{12}{999}+\dfrac{123}{9999}\right)\cdot0\)
\(Q=0\)

\(M=\dfrac{8}{3}\cdot\dfrac{2}{5}\cdot\dfrac{3}{8}\cdot10\cdot\dfrac{19}{92}\\ =\dfrac{8\cdot2\cdot3\cdot10\cdot19}{3\cdot5\cdot8\cdot92}\\ =\dfrac{8\cdot2\cdot3\cdot2\cdot5\cdot19}{3\cdot5\cdot8\cdot2\cdot2\cdot23}\\ =\dfrac{19}{23}\)
\(N=\dfrac{5}{7}\cdot\dfrac{5}{11}+\dfrac{5}{7}\cdot\dfrac{2}{11}-\dfrac{5}{7}\cdot\dfrac{14}{11}\\ =\dfrac{5}{7}\cdot\left(\dfrac{5}{11}+\dfrac{2}{11}-\dfrac{14}{11}\right)\\ =\dfrac{5}{7}\cdot\left(-\dfrac{7}{11}\right)\\ =-\dfrac{5}{11}\)
\(Q=\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right)\cdot\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)\\ =\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right)\cdot\left(\dfrac{3}{6}-\dfrac{2}{6}-\dfrac{1}{6}\right)\\ =\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right)\cdot\left(\dfrac{1}{6}-\dfrac{1}{6}\right)\\ =\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right)\cdot0\\ =0\)
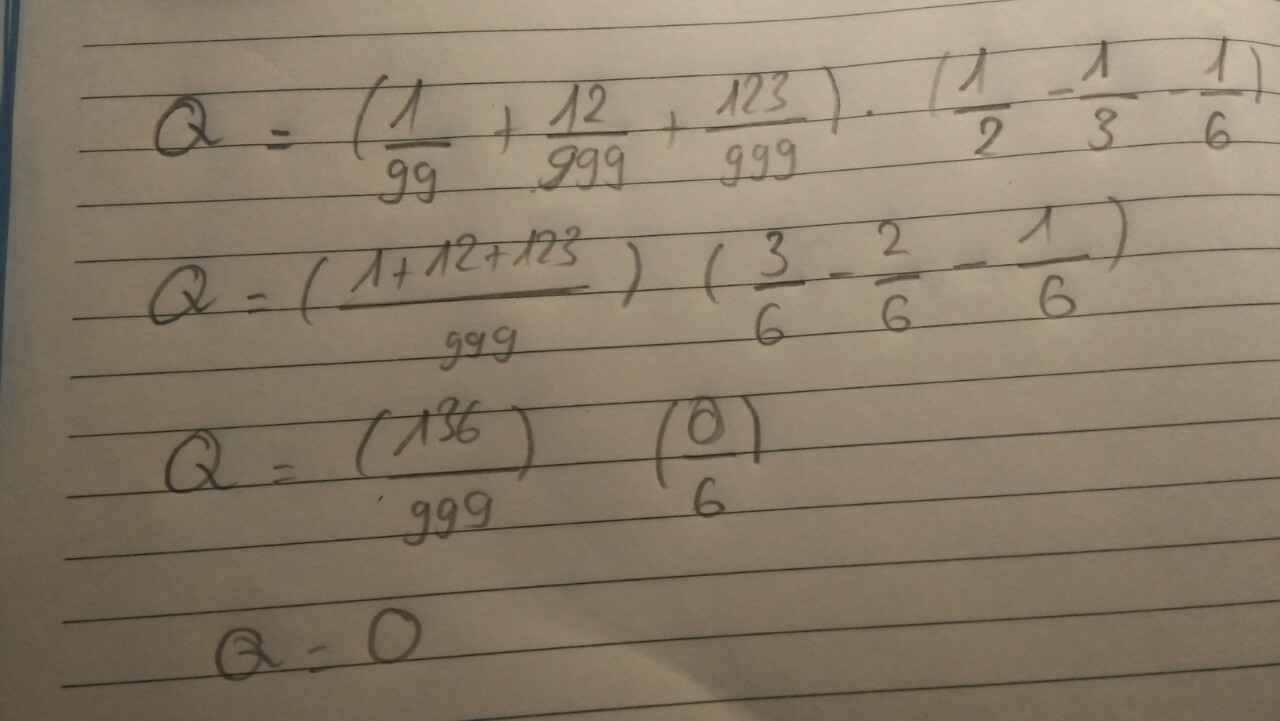
\(\dfrac{1}{1}.\dfrac{1}{2}+\dfrac{1}{2}.\dfrac{1}{3}+\dfrac{1}{3}.\dfrac{1}{4}+...+\dfrac{1}{999}.\dfrac{1}{1000}\\ =\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{999.1000}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{999}-\dfrac{1}{1000}\\ =1-\dfrac{1}{1000}=\dfrac{999}{1000}\)
ta có
1/1.1/2=1-1/2
1/2.1/3=1/2-1/3
1/3.1/4=1/3-1/4
............
1/999.1/1000=1/999-1/1000
Từ đó suy ra
1/1.1/2+1/2-1/3+1/3+.......+1/998.1/999+1/999.1/1000
=1/1-1/2+1/2-1/3+1/3-.....+1/998-1/999+1/999-1/1000
=1-1/1000
=1000/1000-1/1000
=999/1000
nhớ like bạn nhé