tính nhanh : 2/9 + 6/27 + 8/36 +12/54 + 16/72 + 18/81

LD

LINH ĐẬU

20 tháng 9 2020 - olm

Tính nhanh tổng sau:

2/9 + 6/27 + 8/36 + 12/54 + 16/72 + 18/81

#Toán lớp 5

4

NK

Nguyễn Khánh Ly

20 tháng 9 2020

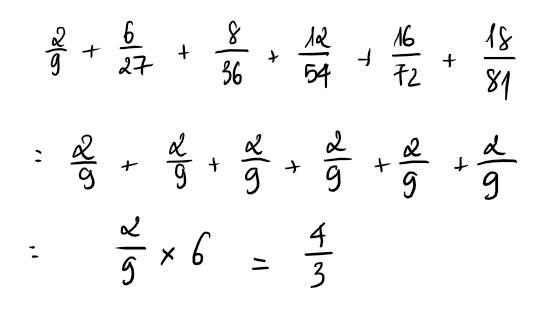
2/9 + 6/27 + 8/36 + 12/54 + 16/72 + 18/81=\(\frac{2}{9}+\frac{2}{9}+\frac{2}{9}+\frac{2}{9}+\frac{2}{9}+\frac{2}{9}\) = \(\frac{2}{9}\). 6 = \(\frac{12}{9}\)= \(\frac{4}{3}\)

Đúng(0)

LA

★luffyッcute★(Team ASL)

20 tháng 9 2020

\(\frac{2}{9}+\frac{6}{27}+\frac{8}{36}+\frac{12}{54}+\frac{16}{72}+\frac{18}{81}\)

\(=\frac{2}{9}+\frac{2}{9}+\frac{2}{9}+\frac{2}{9}+\frac{2}{9}+\frac{2}{9}\)

\(=\frac{2}{9}×6=\frac{4}{3}\)

Đúng(0)

TN

Trần Ngọc Ánh

28 tháng 2 2023

2/9 + 6/27 + 8/36 + 12/54 + 16/72 + 18/81 giúp mình với ( đg cần lắm )

#Toán lớp 5

1

BF

Bacon Family

28 tháng 2 2023

`2/9 + 6/27 + 8/36 + 12/54 + 16/72 + 18/81`

`= 2/9 + 2/9 + 2/9 + 2/9 + 2/9 + 2/9`

`= 2/9 xx 6`

`= 12/9 = 4/3`

Đúng(3)

HK

Hanamaru Kunikida

23 tháng 1 2017 - olm

Tính nhanh:

a) 2/9+6/27+8/36+12/54+16/72+18/81

b) ( 1-2/5) * ( 1-2/7 ) * ( 1-2/9 ) *.....................( 1-2/99)

c) Tính tổng sau bằng cách hợp lí và nhanh nhất

1/2+1/4+1/8+1/16+........................+1/1024

Giúp mik nha các bạn, mik đang cần lắm đó!

#Toán lớp 5

2

NM

Nguyễn Minh Trí

23 tháng 1 2017

a)

Vì 2/9=6/27=8/36=12/54=16/72=18/81 nên:

2/9+6/27+8/36+12/54+16/72+18/81=

2/9+2/9+2/9+2/9+2/9+2/9=

2/9*6=

12/9=

4/3

Vậy 2/9+6/27+8/36+12/54+16/72+18/81=4/3

b)

Ta có:

1-2/5=3/5

1-2/7=5/7

1-2/9=7/9

...

1-2/99=97/99

Vậy (1-2/5)*(1-2/7)*(1-2/9)*...*(1-2/99)=

3/5*5/7*7/9*...*97/99=

(3*5*7*...*97)/(5*7*9*...*99)=

3/99=

1/33

Vậy (1-2/5)*(1-2/7)*(1-2/9)*...*(1-2/99)=1/33

c)

Gọi biểu thức 1/2+1/4+1/8+1/16+...+1/1024 là S,ta có:

S=1/2+1/4+1/8+1/16+...+1/1024

S*2=1+1/2+1/4+1/8+...+1/512

S*2-S=(1+1/2+1/4+1/8+...+1/512)-(1/2+1/4+1/8+1/16+...+1/1024)

S=1-1/1024

S=1023/1024

Vậy 1/2+1/4+1/8+1/16+...+1/1024=1023/1024

Đúng(0)

HK

Hanamaru Kunikida

23 tháng 1 2017

Cảm ơn bạn nhé!

Đúng(0)

MT

Minh tú Trần

28 tháng 6 2018 - olm

a. Tính tổng

1+2+3+4+5+6+7+8+9+10

b. Áp dụng câu a để tính nhanh tổng sau

9+18+27+36+45+54+63+72+81+90

#Toán lớp 5

1

TC

Trần Châu Minh Hạnh

28 tháng 6 2018

a. =(1+10)×10 :2

=11×10:2

=110:2

=55

b. Số các số hạng là =(90-9):9+1= 10

Tổng = (9+90)×10:2=495

Đúng(0)

X

xinhxinh194

22 tháng 10 2017 - olm

Tính nhanh:

a,1/4+2/5+6/8+9/15+8/1

b,1/2+2/4+3/6+4/8+5/10+6/12+7/14+8/16+9/18+10/20

c,1/10+4/20+9/30+16/40+25/50+36/60+49/70+64/80+81/90

#Toán lớp 5

3

NT

Nguyễn Thị Thương Hoài

Giáo viên VIP

27 tháng 7

a; \(\dfrac{1}{4}\) + \(\dfrac{2}{5}\) + \(\dfrac{6}{8}\) + \(\dfrac{9}{15}\) + \(\dfrac{8}{1}\)

= (\(\dfrac{1}{4}\) + \(\dfrac{6}{8}\)) + (\(\dfrac{2}{5}\) + \(\dfrac{9}{15}\)) + \(\dfrac{8}{1}\)

= (\(\dfrac{1}{4}\) + \(\dfrac{3}{4}\)) + (\(\dfrac{2}{5}\) + \(\dfrac{3}{5}\)) + 8

= 1 + 1 + 8

= 2 + 8

= 10

Đúng(0)

NT

Nguyễn Thị Thương Hoài

Giáo viên VIP

27 tháng 7

b; \(\dfrac{1}{2}\) + \(\dfrac{2}{4}\) + \(\dfrac{3}{6}\) + \(\dfrac{4}{8}\) + \(\dfrac{5}{10}\) + \(\dfrac{6}{12}\) + \(\dfrac{7}{14}\) + \(\dfrac{8}{16}\) + \(\dfrac{10}{20}\)

= \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) x (\(\dfrac{2}{2}\) + \(\dfrac{3}{3}\) + \(\dfrac{4}{4}\) + \(\dfrac{5}{5}\)+ \(\dfrac{6}{6}+\dfrac{7}{7}+\dfrac{8}{8}\) + \(\dfrac{10}{10}\))

= \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) x (1 + 1 +1 + 1+ 1+ 1+ 1 +1)

= \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) x 1 x 8

= \(\dfrac{1}{2}\) + \(\)\(\dfrac{1}{2}\) x 8

= \(\dfrac{1}{2}\) + 4

= \(\dfrac{9}{2}\)

Đúng(0)

X

xinhxinh194

22 tháng 10 2017 - olm

Tính nhanh:

a,1/4+2/5+6/8+9/15+8/1

b,1/2+2/4+3/6+4/8+5/10+6/12+7/14+8/16+9/18+10/20

c,1/10+4/20+9/30+16/40+25/50+36/60+49/70+64/80+81/90

#Toán lớp 5

3

NT

Nguyễn Thị Thương Hoài

Giáo viên VIP

21 tháng 9

a; \(\dfrac{1}{4}\) + \(\dfrac{2}{5}\) + \(\dfrac{6}{8}\) + \(\dfrac{9}{15}\) + \(\dfrac{8}{1}\)

= (\(\dfrac{1}{4}\) + \(\dfrac{6}{8}\)) + (\(\dfrac{2}{5}\) + \(\dfrac{9}{15}\)) + 8

= (\(\dfrac{1}{4}\) + \(\dfrac{3}{4}\)) + (\(\dfrac{2}{5}\) + \(\dfrac{3}{5}\)) + 8

= 1 + 1 + 8

= 2 + 8

= 10

Đúng(0)

NT

Nguyễn Thị Thương Hoài

Giáo viên VIP

21 tháng 9

b; \(\dfrac{1}{2}\) + \(\dfrac{2}{4}\) + \(\dfrac{3}{6}\) + \(\dfrac{4}{8}\) + \(\dfrac{5}{10}\) + \(\dfrac{6}{12}\) + \(\dfrac{7}{14}\) + \(\dfrac{8}{16}\) + \(\dfrac{9}{18}\) + \(\dfrac{10}{20}\)

= \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\)

= \(\dfrac{1}{2}\) x 10

= 5

Đúng(0)

NT

Nguyễn Thùy Linh

30 tháng 8 2023 - olm

Bài 2: Viết tiếp 2 số hạng vào dãy số sau: a) 10, 13, 18, 26, ... b) 0, 1, 2, 4, 7, 12, ... c) 0, 1, 4, 9, 18, ... d) 5, 6, 8, 10, ... e) 1, 6, 54, 648, ... ... k) 1, 3, 3, 9, 27, L) 1, 2, 3, 6, 12, 24.... m) 1, 4, 9, 16, 25, 36, o) 2, 12, 30, 56, 90, p) 1, 3, 9, 27, .... g) 1, 5, 14, 33, 72, h) 2, 20, 56, 110, 182..... q) 2, 6, 12, 20, 30, ... t) 6, 24, 60, 120,...

Đọc tiếp

#Toán lớp 5

2

NT

Nguyễn Thùy Linh

30 tháng 8 2023

cứu

Đúng(1)

ND

Nguyễn Đức Trí

31 tháng 8 2023

a) 10; 13; 18; 26; 36; 52...

c) 0; 1; 4; 9; 16; 25...

m) 1; 4; 9; 16; 25; 36; 49; 64...

p) 1; 3; 9; 27; 81; 243...

Đúng(1)

LL

lưu lê thanh bình

8 tháng 3 2020 - olm

tính nhanh

1*3*9+2*6*18+3*9*27/1*5*18+2*10*36+3*15*54

#Toán lớp 5

1

IA

I am➻Minh

8 tháng 3 2020

\(\frac{1\cdot3\cdot9+2\cdot6\cdot18+3\cdot9\cdot27}{1\cdot5\cdot18+2\cdot10\cdot36+3\cdot15\cdot54}\)

\(=\frac{1\cdot3\cdot9+2\left(1\cdot3\cdot9\right)+3\left(1\cdot3\cdot9\right)}{1\cdot5\cdot18+2\left(1\cdot5\cdot18\right)+3\left(1\cdot5\cdot18\right)}\)

\(=\frac{\left(1\cdot3\cdot9\right)\left(1+2+3\right)}{\left(1\cdot5\cdot18\right)\left(1+2+3\right)}\)

\(=\frac{3}{10}\)

Đúng(0)

NT

Nguyễn Thu Huyền

16 tháng 8 2018 - olm

Viết thêm 2 số hạng vào dãy số:a) 10, 13, 18, 26, … k) 1, 3, 3, 9, 27, …b) 0, 1, 2, 4, 7, 12, … l) 1, 2, 3, 6, 12, 24,....c) 0, 1, 4, 9, 18, … m) 1, 4, 9, 16, 25, 36, …d) 5, 6, 8, 10, … o) 2, 12, 30, 56, 90, …e) 1, 6, 54, 648, … p) 1, 3, 9, 27, …g) 1, 5, 14, 33, 72, … q) 2, 6, 12, 20, 30, …h) 2, 20, 56, 110, 182,…. t) 6, 24, 60, 120,...

Đọc tiếp

#Toán lớp 5

1