Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: CO = CA (gt)
DO = DB (gt)
⇒ CD là đường trung bình của ΔOAB
⇒ AB = 2CD = 2.3 = 6cm.

Bài giải:
Ta có CO = CA (gt)
DO = DB (gt)
Nên CD là đường trung bình của ∆OAB.
Do đó CD = 1212AB
Suy ra AB = 2CD = 2.3 = 6cm.
Ta có: CO = CA (gt)
DO = DB (gt)
Nên CD là đường trung bình của ΔOAB
Suy ra AB = 2CD = 2.3 = 6cm

Xét tam giác OAB ta có:
C là trung điểm của OA (1)
D là trung điểm của OB (2)
Từ (1)(2) => CD là đường trung bình của tam giác OAB
=> CD=1/2AB
=>AB = CD x 2 =5 x 2 =10 (cm )
P/s tham khảo nha

a)
Vẽ hình đúng đến câu a

Lập luận được điểm A nằm giữa hai điểm O và B
Tính được AB = 6cm
b)Lập luận chứng tỏ được A là trung điểm của đoạn thẳng OB
Lập luận tính được OM = 3cm
c)Lập luận chứng tỏ điểm M nằm giữa hai điểm O và B
Suy ra OM + MB = OB
Tính MB = 9cm
d)Lập luận chứng tỏ được điểm O nằm giữa hai điểm M và N
Chỉ ra được OM = ON và kết luận ) là trung điểm của đoạn thẳng MN
Vì OA=6,OB=12 nên AB=12-6=6
Vì OA<OB(6<12) suy ra A nằm giữa O và B 1
Mà OA=6,AB=6 2
Từ 1 và 2 suy ra A là trung điểm của đoạn thẳng OB
Vì M là trung điểm của OA nên OM=OA/2=3
Ta có OM=3,OB=12 nên MB=12-3=9
Vì ON thuộc tia đối của tia Ox nên O nằm giữa N và M 3
Lại có OM=ON=3 4
Từ 3 va 4 suy ra O là trung điểm của MN

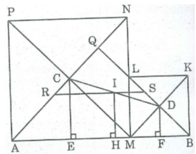
Kẻ CE ⊥ AB, IH ⊥ AB, DF ⊥ AB
Suy ra: CE // DF // IH
IC = ID (gt)
Nên IH là đường trung bình của hình thang DCEF ⇒ IH = (DF + CE) / 2
Vì C là tâm hình vuông AMNP nên ∆ CAM vuông cân tại C
CE ⊥ AM ⇒ CE là đường trung tuyến (tính chất tam giác cân)
⇒ CE = 1/2 AM
Vì D là tâm hình vuông BMLK nên ∆ DBM vuông cân tại D
DF ⊥ BM ⇒ DF là đường trung tuyến (tính chất tam giác cân)
⇒ DF = 1/2 BM
Vậy CE + DF = 1/2 AM + 1/2 BM = 1/2 (AM + BM)= 1/2 AB = a/2
Suy ra: IH = (a/2) / 2 = a/4
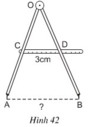
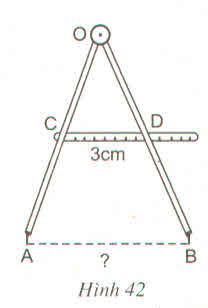


Ta có: CD là đường trung bình của \(\Delta OAB\) (C, D lần lượt là trung điểm của OA, OB)
\(\Rightarrow CD=\dfrac{AB}{2}\)
\(\Rightarrow AB=2.CD=2.3=6\left(cm\right).\)