Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(2^3\times2+3^{15}\div3^{13}+2020^0\)
\(=2^4+3^2+1\)
\(=16+9+1=26\)
\(2^3\times15-[115-\left(12-5\right)^2]\)
\(=8\times15-\left(115-7^2\right)\)
\(=120-115+49\)
\(=5+49=54\)

a, a = BCNN(15;115) = 345
b, a – 1 ∈ BC(35;52) và 999 < a – 1 < 1999
Ta có BCNN(35;52) = 35.52 = 1820
Suy ra a – 1 ∈ {0;1820;3640;...}
Vì 999 < a – 1 < 1999 nên a – 1 = 1820
a = 1821

a) \(x⋮15;x⋮35;x⋮42\&250< x< 850\) (sửa dấu chia thành chia hết)
\(BCNN\left(15;35;42\right)=210\)
\(\Rightarrow x\in BC\left(15;35;42\right)=\left\{0;210;420;630;840;...\right\}\)
mà \(250< x< 850\)
\(\Rightarrow x\in\left\{420;630;840\right\}\)
b) x nhỏ nhất khác 0 thỏa mãn \(x⋮15;x⋮115\)
\(BCNN\left(15;115\right)=345\)
Vậy \(x\in\left\{345\right\}\) thỏa mãn đề bài

a ) A = 5 6
b ) B = 10 39 c ) C = 1 3.5 + 1 5.7 + 1 7.9 + 1 9.11 + 1 11.13 = 1 2 1 3 − 1 13 = 5 39
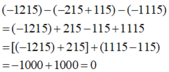
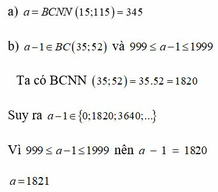


Đáp án là C