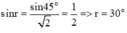Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ \(n\sin i=\sin r\Leftrightarrow n\sin i=\cos i\left(r=90^0-i\right)\)
\(\Rightarrow\tan i=\dfrac{1}{n}=\dfrac{1}{\sqrt{3}}\Rightarrow i=\dfrac{\pi}{6}\)
b/ \(i\ge i_{gh};\sin i_{gh}=\dfrac{1}{n}\Leftrightarrow\sin45=\dfrac{1}{n}\Rightarrow n=\sqrt{2}\)

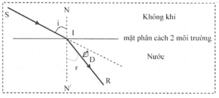
a) Góc khúc xạ:
Ta có: \(n_1.sin\left(i\right)=n_2.sin\left(r\right)\)
\(\Leftrightarrow1.sin\left(60\right)=1,5.sin\left(r\right)\)
\(\Leftrightarrow r\approx35^o\)
b) Góc lệch D tạo bởi tia khúc và tia tới:
\(D=i-r\)
\(\Leftrightarrow D=60-35\)
\(\Leftrightarrow D=25^o\)

\(\sin i=n.\sin r\Rightarrow n=\dfrac{\sin i}{\sin r}\)
\(\sin i'=n.\sin r'\Rightarrow n=\dfrac{\sin i'}{\sin r'}\)
\(i+i'=90^0\Rightarrow\sin i'=\cos\left(90^0-i'\right)=\cos i\)
\(\Rightarrow\dfrac{\sin i}{\sin r}=\dfrac{\cos i}{\sin r'}\Leftrightarrow\dfrac{\sin i}{\sin30^0}=\dfrac{\cos i}{\sin45^0}\)
\(\Leftrightarrow\sin i-\dfrac{\sqrt{2}}{2}\cos i=0\)
\(\cos x=0\) ko la nghiem pt
\(\cos x\ne0\Rightarrow\tan i-\dfrac{\sqrt{2}}{2}=0\Rightarrow\tan i=\dfrac{\sqrt{2}}{2}\Rightarrow i\approx35^0\)
\(\Rightarrow n=\dfrac{\sin i}{\sin r}=\dfrac{\sin35^0}{\sin30^0}\approx1,15\)
\(\)
\(\)

Đáp án: A
Để tia phản xạ vuông góc với tia tới thì góc tới i = 45 0
Áp dụng định luật khúc xạ ta được: