Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án
Bài giải qua 3 bước như sau:
Bước 1: Xét mẫu số của số hạng tổng quát trong tổng trên:
S = 1 + 2 + ... + (n - 1) + n ( * )
Khi viết S theo thứ tự ngược lại la có:
S = n + (n - 1) + ... + 2 + 1 ( ** )
Cộng vế với vế của ( * ) và ( ** ) ta có:
S + S = [1 + n] + [2 + (n - 1)] + ... + [(n - 1) + 2] + [n + 1]
2 . S = [n + 1] + [n + 1] + . . . + [n + 1] + [n + 1] (Tổng có n số hạng [n + 1] )
2 . S = n.(n + 1)
=> S = n.(n + 1)/2
=> Số hạng tổng quát của tổng đã cho là:
Bước 2: Ta có nhận xét:
=> ( *** )
Bước 3: Thay n = 1, 2, ... vào ( *** ) ta được các đẳng thức tương ứng:
. . .
Cộng các vế với nhau ta được:
Vậy tổng đã cho có kết quả bằng 2.
Đặng Thị Thùy Linh copy đáp án trên OLM
bn có thể vào mục "toán vui mỗi tuần" của OLM

Đáp án B
S n = 1 − 1 2 2 1 − 1 3 2 ... 1 − 1 n 2 = 1 − 1 2 1 − 1 3 ... 1 − 1 n × 1 + 1 2 1 + 1 3 ... 1 + 1 n
1 − 1 2 1 − 1 3 ... 1 − 1 n = 1 2 . 2 3 ... n − 1 n = 1 n 1 + 1 2 1 + 1 3 ... 1 + 1 n = 3 2 . 4 3 ... n + 1 n = n + 1 2 ⇒ S n = 1 n . n + 1 2 = n + 1 2 n lim S n = lim n + 1 2 n = lim 1 + 1 n 2 = 1 2

Bài 2 :
Ta có :
\(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}=\left(1-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{4}\right)+\left(\frac{1}{4}-\frac{1}{8}\right)+\left(\frac{1}{8}-\frac{1}{16}\right)+\left(\frac{1}{16}-\frac{1}{32}\right)\)
\(=1-\frac{1}{32}\)
và \(B=\frac{2003}{2004}=1-\frac{1}{2004}\)
Vì \(\frac{1}{32}>\frac{1}{2004}\) nên A < B

B= 3/2.4/3. ....2001/2000
B = 3.4....2001/2.3....2000
B =2001/2
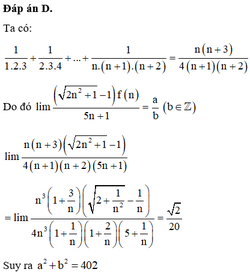
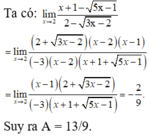
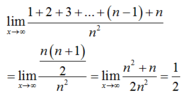
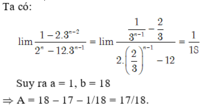
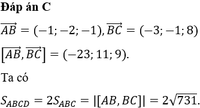
Đáp án B
lim 1 − 1 2 2 1 − 1 3 2 ... 1 − 1 n 2 = lim 1.3 2 2 . 2.4 3 2 . 3.5 4 2 ... n − 1 n + 1 n 2 = lim 1 2 . n + 1 n = 1 2