DQ
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DV
1
TY
1
12 tháng 10 2015
ta có : (x-y)2=16
x2-2xy+y2=16
x2+y2=5.2+16
x2+2xy+y2-2xy=26
(x+y)2-2.5=26
(x+y)2-10=26
(x+y)2=26+10=36
suy ra x+y=6
x+y= -6
ta có nếu: x-y=4=>y=x -4
=>x+y= -6
<=>x+x -4= -6
2x= -2=>x= -1
nếu x+y=6
<=>x+x -4=6
2x=10
=> x=5
mà x<0 => x+y=-6
24 tháng 8 2017
HD:
Dễ thấy b = 1, d = 2, e = 4 đặt y = x2 – 2 suy ra y2 = x4 – 4x2 + 4
Biến đổi P(x) = x4 – 4x2 + 4 – x3 – 6x2 + 2x
= (x2 – 2)2 – x(x2 – 2) – 6x2
Từ đó Q(y) = y2 – xy – 6x2
Tìm m, n sao cho m.n = - 6x2 và m + n = - x chọn m = 2x, n = -3x
Ta có: Q(y) = y2 + 2xy – 3xy – 6x2
= y(y + 2x) – 3x(y + 2x)
= (y + 2x)(y – 3x)
Do đó: P(x) = (x2 + 2x – 2)(x2 – 3x – 2).
DA
24 tháng 8 2017
a/ tìm GT của x+y biết x-y=2; x.y=99 và y<0
Vì x-y=2 nên
\(\Leftrightarrow\)
\(\Leftrightarrow\)
\(\Leftrightarrow\)
\(\Leftrightarrow\)
\(\Leftrightarrow\) x+y=20 hoặc x+y=-20
mà y<0 nên x+y=20
25 tháng 11 2020
Bạn tham khảo bài này nha
Link:https://olm.vn/hoi-dap/detail/266831819020.html
Chúc bạn học tốt
PN
8 tháng 4 2016
\(a.\)
Phân tích biển đổi thành nhân tử kết hợp với chuyển vế để quy về hẳng đẳng thức, khi đó, ta tính được \(a,b\)
Thật vậy, ta có:
\(a^2-2a+6b+b^2=-10\)
\(\Leftrightarrow\) \(a^2-2a+6b+b^2+10=0\)
\(\Leftrightarrow\) \(\left(a^2-2a+1\right)+\left(b^2+6b+9\right)=0\)
\(\Leftrightarrow\) \(\left(a-1\right)^2+\left(b+3\right)^2=0\) \(\left(1\right)\)
Vì \(\left(a-1\right)^2\ge0;\) \(\left(b+3\right)^2\ge0\) với mọi \(a,b\)
nên để thỏa mãn đẳng thức \(\left(1\right)\) thì phải xảy ra đồng thời \(\left(a-1\right)^2=0\) và \(\left(b+3\right)^2=0\)
\(\Leftrightarrow\) \(a-1=0\) và \(b+3=0\) \(\Leftrightarrow\) \(a=1\) và \(b=-3\)
\(b.\) Cộng \(1\) vào mỗi phân thức của biểu thức \(A\), khi đó, ta có:
\(A+3=\left(\frac{x+y}{z}+1\right)+\left(\frac{x+z}{y}+1\right)+\left(\frac{y+z}{x}+1\right)=\frac{x+y+z}{z}+\frac{x+y+z}{y}+\frac{x+y+z}{x}\)
\(A+3=\left(x+y+z\right)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)=0\) (do \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0\))
Vậy, \(A=-3\)
AD
0
AH
Akai Haruma
Giáo viên
16 tháng 12 2021
Bài 1:
$2xy=(x+y)^2-(x^2+y^2)=4^2-10=6\Rightarrow xy=3$
$M=x^6+y^6=(x^3+y^3)^2-2x^3y^3$
$=[(x+y)^3-3xy(x+y)]^2-2(xy)^3=(4^3-3.3.4)^2-2.3^3=730$
AH
Akai Haruma
Giáo viên
16 tháng 12 2021
Bài 2:
$8x^3-32y-32x^2y+8x=0$
$\Leftrightarrow (8x^3+8x)-(32y+32x^2y)=0$
$\Leftrightarrow 8x(x^2+1)-32y(1+x^2)=0$
$\Leftrightarrow (8x-32y)(x^2+1)=0$
$\Rightarrow 8x-32y=0$ (do $x^2+1>0$ với mọi $x$)
$\Leftrightarrow x=4y$
Khi đó:
$M=\frac{3.4y+2y}{3.4y-2y}=\frac{14y}{10y}=\frac{14}{10}=\frac{7}{5}$
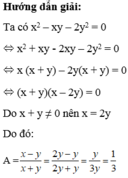
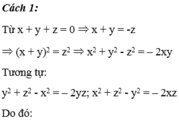
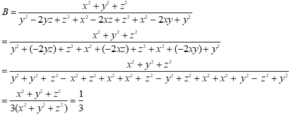
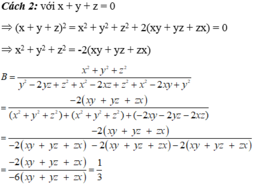
\(y^3-\frac{1}{8}=0\Leftrightarrow y^3-\left(\frac{1}{2}\right)^3=0\)
\(\Leftrightarrow\left(y-\frac{1}{2}\right)\left(y^2+\frac{1}{2}y+\frac{1}{4}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}y-\frac{1}{2}=0\\y^2+\frac{1}{2}y+\frac{1}{4}=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}y=\frac{1}{2}\\y^2+2.\frac{1}{4}y+\frac{1}{16}+\frac{3}{16}=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}y=\frac{1}{2}\\\left(y+\frac{1}{4}\right)^2+\frac{3}{16}=0\left(vôlí\right)\end{cases}}\)
Vậy \(y=\frac{1}{2}\)