K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CH
Cô Hoàng Huyền
Admin
VIP
31 tháng 7 2017
Ta thấy \(4x^2+17xy+9y^2=5xy-\left|y-2\right|\)
\(\Leftrightarrow4x^2+12xy+9y^2=-\left|y-2\right|\Leftrightarrow\left(2x+3y\right)^2=-\left|y-2\right|\)
Do \(\left(2x+3y\right)^2\ge0;-\left|y-2\right|\le0\) nên dấu bằng xảy ra khi và chỉ khi \(\hept{\begin{cases}y-2=0\\2x+3y=0\end{cases}}\Rightarrow\hept{\begin{cases}y=2\\x=-3\end{cases}}\)
Thay vào M ta có \(M=\left(-3\right)^3+2.2+3.\left(-3\right)^2.2=31\)
OB
4
24 tháng 9 2016
ta có 2x2+2y2=5xy
=>2(x+y)2=9xy và 2(x-y)2=xy
M2=\(\frac{\left(x+y\right)^2}{\left(x-y\right)^2}=\frac{9xy}{xy}=9\)
vậy M=3 hoặc M=-3
25 tháng 9 2016
Ta dùng phương pháp tách đa thức thành nhân tử ta được
=> x+y=2x2+2y2=2(x2+y2)=9xy
=> x-y=2x2-2y2=2(x2-y2)=xy=1xy=xy
=>M=(x+y)2/(x-y)2=9xy:xy=9
Nên M= cộng trừ căn bậc 2 của 9
NM
Nguyễn Minh Quang
Giáo viên
9 tháng 9 2021
Bài 1
ta có a+3+b-3 =a +b chia hết cho 4
nên (b-a )(a+b) cũng chia hết cho 4
bài 2.
ta có: \(M=6x^2-5x-6-12xy+6y^2+6y-3x+2y+2027\)
\(=6\left(x-y\right)^2-8\left(x-y\right)+2021=24-16+2021=2029\)
PT
1
CM
29 tháng 1 2019
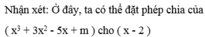
để tìm số dư, rồi cho số dư đó bằng 0, từ đó tìm được giá trị của m.
Mở rộng: Bài toán này ta áp dụng phân tích đa thức thành nhân tử để giải toán
MN
1
12 tháng 11 2021
\(\Leftrightarrow8x^3-2x^2-15x+m=\left(4x-3\right)\cdot a\left(x\right)\)
Thay \(x=\dfrac{3}{4}\Leftrightarrow8\cdot\left(\dfrac{3}{4}\right)^3-2\left(\dfrac{3}{4}\right)^2-15\cdot\dfrac{3}{4}+m=0\)
\(\Leftrightarrow8\cdot\dfrac{27}{64}-2\cdot\dfrac{9}{16}-\dfrac{45}{4}+m=0\\ \Leftrightarrow\dfrac{27}{8}-\dfrac{9}{8}-\dfrac{45}{4}+m=0\\ \Leftrightarrow\dfrac{9}{4}-\dfrac{45}{4}+m=0\\ \Leftrightarrow m-9=0\\ \Leftrightarrow m=9\)
K
2
9 tháng 1 2022
\(\Leftrightarrow6x^2+4x-9x-6+m+4⋮3x+2\)
=>m+4=0
hay m=-4
9 tháng 1 2022
6x2−5x+a=(6x2−5x−6)+a+6=(3x+2)(2x−3)+a+66x2−5x+a=(6x2−5x−6)+a+6=(3x+2)(2x−3)+a+6
Do (3x+2)(2x−3)⋮3x+2(3x+2)(2x−3)⋮3x+2 nên đa thức đã cho chia hết 3x+2 khi và chỉ khi:
a+6=0⇒a=−6
27 tháng 7 2016
Bài 4 :
Thay x=y+5 , ta có :
a ) ( y+5)*(y5+2)+y*(y-2)-2y*(y+5)+65
=(y+5)*(y+7)+y^2-2y-2y^2-10y+65
=y^2+7y+5y+35-y^2-2y-2y^2-10y+65
= 100
Bài 5 :
A = 15x-23y
B = 2x-3y
Ta có : A-B
= ( 15x -23y)-(2x-3y)
=15x-23y-2x-3y
=13x-26y
=13x*(x-2y) chia hết cho 13
=> Nếu A chia hết cho 13 thì B chia hết cho 13 và ngược lại
CM
21 tháng 10 2018
a) Tìm mẫu thức chung rồi xét mẫu thức chung khác 0 rút được x ≠ ± 1 .
b) Thực hiện phép tính để thu gọn M chúng ta có M = 1 3
Để 32x²y^m chia hết cho -5xy² thì m ≥ 2