Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thay x = 1; y = -1; z = 3 vào biểu thức, ta có:
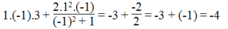
Vậy giá trị của biểu thức xyz + 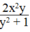 bằng -4 tại x = 1; y = -1; z = 3
bằng -4 tại x = 1; y = -1; z = 3

B=(xyz)+(xyz)^2+(xyz)^3+...+(xyz)^100
=(-1)+1+(-1)+1+...+(-1)+1
=0

a, 3y(x2-xy)-7x2(y+xy)
= 6xy - 3xy2 - 14xy - 14x2y
=-8xy-3xy2-14x2y
Bậc: 2

a.A=xy+x2y2+x3y3...+x100y100
-1.-1+-12.-12+-13.-13+....+-1100-1100
=1+1+-1+....+1
=1+0+0+...+0+1
=1+1=2
b.
B=xyz=x2y2z2+x3y3z3+....+x10y10z10
thay x=-1;y=-1;z=-1
B=(-1).(-1).(-1)=(-1)2.(-1)2.(-1)2+(-1)3.(-1)3.(-1)3+....+(-1)10.(-1)10.(-1)10
B=-1=1+(-1)+...+1
B=-1=0+...+0
B=0

a)
Ta có \(xy+x^2y^2+x^3y^3+...+x^{10}y^{10}\\ =\left(xy+x^3y^3+x^5y^5+...+x^9y^9\right).\left(x^2y^2+x^4y^4+x^6y^6+...+x^{10}y^{10}\right)\)
Thay x= -1 và y= 1 vào biểu thức trên ta được\(\left(-1\right)1+\left(-1\right)^21^2+...+\left(-1\right)^{10}1^{10}\\ =\left[\left(-1\right)1+\left(-1\right)^31^3+...+\left(-1\right)^91^9\right].\left[\left(-1\right)^21^2+\left(-1\right)^41^4+...+\left(-1\right)^{10}1^{10}\right]\\ =\left(-1-1-...-1\right)+\left(1+1+...+1\right)\\ =-5+5=0\)
b)
Ta có:\(xyz+x^2y^2z^2+x^3y^3z^3+...+x^{10}y^{10}z^{10}\\ =\left(xyz+x^3y^3z^3+x^5y^5z^5+...+x^9y^9z^9\right).\left(x^2y^2z^2+x^4y^4z^4+x^6y^6z^6+...+x^{10}y^{10}z^{10}\right)\)
Thay x=1; y= -1 và z= -1 vào biểu thức trên ta được\(\left(-1\right)\left(-1\right)1+\left(-1\right)^2\left(-1\right)^21^2+...+\left(-1\right)^{10}\left(-1\right)^{10}1^{10}\\ =\left[\left(-1\right)\left(-1\right)1+\left(-1\right)^3\left(-1\right)^31^3+...+\left(-1\right)^9\left(-1\right)^91^9\right].\left[\left(-1\right)^2\left(-1\right)^21^2+\left(-1\right)^4\left(-1\right)^41^4+...+\left(-1\right)^{10}\left(-1\right)^{10}1^{10}\right]\\ =\left(1+1+...+1\right)+\left(1+1+...+1\right)\\ =5+5=10\)
Ta có xy+x2y2+x3y3+...+x10y10=(xy+x3y3+x5y5+...+x9y9).(x2y2+x4y4+x6y6+...+x10y10)xy+x2y2+x3y3+...+x10y10=(xy+x3y3+x5y5+...+x9y9).(x2y2+x4y4+x6y6+...+x10y10)
Thay x= -1 và y= 1 vào biểu thức trên ta được(−1)1+(−1)212+...+(−1)10110=[(−1)1+(−1)313+...+(−1)919].[(−1)212+(−1)414+...+(−1)10110]=(−1−1−...−1)+(1+1+...+1)=−5+5=0(−1)1+(−1)212+...+(−1)10110=[(−1)1+(−1)313+...+(−1)919].[(−1)212+(−1)414+...+(−1)10110]=(−1−1−...−1)+(1+1+...+1)=−5+5=0
b)
Ta có:xyz+x2y2z2+x3y3z3+...+x10y10z10=(xyz+x3y3z3+x5y5z5+...+x9y9z9).(x2y2z2+x4y4z4+x6y6z6+...+x10y10z10)xyz+x2y2z2+x3y3z3+...+x10y10z10=(xyz+x3y3z3+x5y5z5+...+x9y9z9).(x2y2z2+x4y4z4+x6y6z6+...+x10y10z10)
Thay x=1; y= -1 và z= -1 vào biểu thức trên ta được(−1)(−1)1+(−1)2(−1)212+...+(−1)10(−1)10110=[(−1)(−1)1+(−1)3(−1)313+...+(−1)9(−1)919].[(−1)2(−1)212+(−1)4(−1)414+...+(−1)10(−1)10110]=(1+1+...+1)+(1+1+...+1)=5+5=10

Thay `x = -1 ; y = 2` vào `A`, có:
`A = (-1)^2 . 2^3 + (-1) . 2`
`A = 1 . 8 - 1 . 2 = 6`
________________________________
Thay `x = 3 ; y = 2 ; z = 1` vào `B`. Ta có:
`B = 2 . 3^2 + 2^4 + 3 . 2 . 1 - 5`
`B = 2 . 9 + 16 + 6 - 5`
`B = 18 + 16 + 6 - 5 = 35`
Thay x=−1;y=2x=-1;y=2 vào A,
Ta có:A=(−1)2.23+(−1).2
A=(-1)2.23+(-1).2
A=1.8−1.2=6
A=1.8-1.2=6
________________________________
Thay x=3;y=2;z=1x=3;y=2;z=1 vào B.
Ta có:B=2.32+24+3.2.1−5
B=2.32+24+3.2.1-5
B=2.9+16+6−5B=2.9+16+6-5
B=18+16+6−5=35
Ta có: xyz + x2y2z2 + x3y3z3 + ….. + x10y10z10
= xyz + (xyz)2 + (xyz)3 + ….. + (xyz)10
Với x = 1; y = -1; z = - 1 ta có: xyz = 1.(-1).(-1) = 1
Thay vào đa thức: 1 + 12 + 13 + … + 110 = 10