Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2) Ta có:
\(B=x^4+2x^3y-2x^3+x^2y^2-2x^2y-x\left(x+y\right)+2x+3\)
\(=x^4+x^3y-2x^3+x^3y+x^2y^2-2x^2y-x\left(x+y\right)+2x+3\)
\(=\left(x^4+x^3y-2x^3\right)+\left(x^3y+x^2y^2-2x^2y\right)-\left[x\left(x+y\right)-2x\right]+3\)
Do \(x+y-2=0\Rightarrow x+y=2\)
\(\Rightarrow B=\left(x^4+x^3y-2x^3\right)+\left(x^3y+x^2y^2-2x^2y\right)-\left[2x-2x\right]+3\)
\(=x^3.\left(x+y-2\right)+x^2y\left(x+y-2\right)-0+3\)
\(=0+0+3\)
\(=3\)
Vậy \(B=3\)
1) Ta có:
\(A=x^3+x^2y-2x^2-xy-y^2+3y+x-1\)
\(=\left(x^3+x^2y-2x^2\right)-\left(xy+y^2-2y\right)+y+x-1\)
\(=x^2\left(x+y-2\right)-y\left(x+y-2\right)+\left(x+y-2\right)+1\)
\(=0+0+0+1\)
\(=1\)
Vậy \(A=1\)

áp án B
Ta có: log 3 x + 1 y + 1 y + 1 = 9 − x − 1 y + 1 ⇔ y + 1 log 3 x + 1 y + 1 + x − 1 y + 1 = 9
⇔ y + 1 log 3 c + 1 y + 1 + x + 1 y + 1 − 2 y = 11
⇔ y + 1 log 3 c + 1 y + 1 − 2 = 9 − x + 1 y + 1 *
Nếu x + 1 y + 1 > 9 ⇒ V T * > 0 ; V P * < 0
Ngược lại nếu x + 1 y + 1 < 9 ⇒ V T * < 0 ; V P * > 0
Do đó * ⇔ x + 1 y + 1 = 9 ⇔ x y + x + y = 8
Khi đó P = x + y 3 − 3 x y x + y − 57 x + y = x + y 3 − 3 8 − x − y x + y − 57 x + y
Đặt t = x + y ≥ 2 ⇒ f t = t 3 − 3 8 − t t − 57 t = t 3 + 3 t 2 − 81 t
⇒ f ' t = 3 t 2 + 6 t − 81 = 0 ⇒ t = − 1 + 2 7 ⇒ P min = f − 1 + 2 7 = 83 − 112 7 ⇒ a + b = − 29

a) A=2x^2-1/3y
thay x=2 và y=9 vào biểu thức:
Ta có :2.2^2-1/3.9
=2.4-3
= 6-3=3
Vậy tại x =2 và y=9 giá trị của biểu thức bằng 3

ta có
\(\)\(y=\frac{1}{3}\log^3_{\frac{1}{2}}x+\log^2_{\frac{1}{2}}x-3\log_{\frac{1}{2}}x+1\)
Đặt =\(t=\log_{\frac{1}{2}}x\) ta có
\(y=\frac{1}{3}t^3+t^2-3t+1\)
với \(\frac{1}{4}\le x\le4\Leftrightarrow\frac{1}{4}\le\left(\frac{1}{2}\right)^t\le4\Leftrightarrow-2\le t\le2\)
thay vì tính GTLN,GTNN của hàm số y trên [1/4;4] ta tính GTLN,GTNN của hàm số trên [-2;2]
ta tính \(y'=t^2+2t-3\)
ta tính y'=0 suy ra t=1(loại);t=-3(loại)
ta tính y(2)=\(\frac{5}{3}\);y(-2)=\(\frac{-25}{3}\)
vậy GTNN của y=\(\frac{-25}{3}khi\log_{\frac{1}{2}}x=-2\Rightarrow x=4\)
hàm số đạt GTLN y=\(\frac{5}{3}\) khi \(\log_{\frac{1}{2}}x=2\Leftrightarrow x=\left(\frac{1}{2}\right)^2=\frac{1}{4}\)

Đáp án A
Ta có: x = 1 ⇒ y = - 2 ⇒ - 2 = 1 + b a - 2 ⇔ - 2 a + 4 = b + 1 ⇔ 2 a + b = 3
Do tiếp tuyến A song song với đường thẳng d : 3 x + y - 4 = 0 hay y = - 3 x + 4 nên y ' 1 = - 2 - a b a - 2 2 = - 3 ⇒ - 2 - a 3 - 2 a a - 2 2 = - 3 ⇔ - 2 a 2 + 3 a + 2 a - 2 2 = - 3 ⇔ a - 2 - 2 a - 1 a - 2 2 = - 3
⇔ - 2 a - 1 = - 3 ⇔ a = 1 ⇒ b = 1 ⇒ a - 3 b = - 2
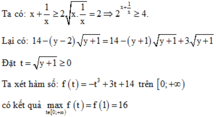
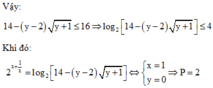



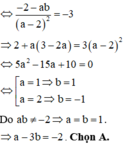
Đáp án B
Ta có x 2 + 1 x 2 - 1 ≥ 2 x 2 . 1 x 2 - 1 = 1 ⇒ 4 x 2 + 1 x 2 - 1 ≥ 4 14 - y - 2 y + 1 ≤ 16 ⇒ log 2 14 - y - 2 y + 1 ≤ 4
Theo giả thiết 4 x 2 + 1 x 2 - 1 = log 2 14 - y - 2 y + 1 ⇒ x 2 = 1 x 2 y = 0 ⇔ x 2 = 1 y = 0
Vậy giá trị biểu thức P = x 2 + y 2 - x y + 1 = 2 .