Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
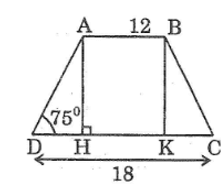
Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm,góc D = 75o
Kẻ AH ⊥ CD, BK ⊥ CD
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Ta có: ∆ADH = ∆BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK

A=(sin220°+sin270°)+(sin230°+sin260°)
+(sin240°+sin250°)-tan245°
=(sin220°+cos220°)+(sin230°+cos230°)+(sin240°+cos240°)-1
=1+1+1-1=2

a, - TXĐ : R ( y = x - 3 )
+, Cho x = 0 -> y = -3 -> Điểm ( 0 ; -3 )
+, Cho y = 0 -> x = 3 -> Điểm ( 3 ; 0 )
- TXĐ : R (y = - x - 1 )
+, Cho x = 0 -> y = -1 -> Điểm ( 0 ; -1 )
+, Cho y = 0 -> x = -1 -> Điểm ( -1 ; 0 )
b, +, Ta có : a1 > 0
=> Tan A1 = a1
=> Tan A1 = 1
=> góc A1 = 45 o
Mà góc A1 và góc OAC là 2 góc đối đỉnh
=> góc A1 = góc OAC = 45o
+, Ta có : a2 < 0
=> Tan ( 180 o - B1 ) = / a2 /
=> Tan ( 180 o - B1 ) = 1
=> góc B1 = 135 o
Mà B1 + ABC = 180 O
=> ABC = 45 o
+, Ta có : ABC + BAC + BCA = 180 O
=> BCA = 90o
Đồ thị hàm số :

Đầu tiên là phải biết quy tắc: ở các góc nhọn, nếu độ lớn của góc tăng thì sin và tan đều tăng
\(sin10^0< sin35^0=cos55^0< sin50^0< tan50^0=cot40^0< tan70^0\)
Lý do \(sin50^0< tan50^0\):
\(tan50^0=\frac{sin50^0}{cos50^0}\) mà \(0< cos50^0< 1\Rightarrow\frac{sin50^0}{cos50^0}>sin50^0\Rightarrow tan50^0>sin50^0\)

a) Ta có: cot 3 độ= tan 87 độ; cot 18 độ= tan 72độ
-> tan 87 độ > tan 72 độ > tan 56 độ > tan 42 độ
vậy cot3 độ> cot 18 độ> tan 56độ> tan 42 độ

a/ \(\left\{{}\begin{matrix}2a+b=1\\5a+b=-\frac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\frac{1}{2}\\b=2\end{matrix}\right.\)
b/ Theo câu a, ta có pt MN là: \(y=-\frac{1}{2}x+2\)
Giao điểm của MN với Ox:
\(y=0\Rightarrow-\frac{1}{2}x+2=0\Rightarrow x=4\Rightarrow A\left(4;0\right)\)
Giao điểm MN với trục Oy:
\(x=0\Rightarrow y=2\Rightarrow B\left(0;2\right)\)

1) Bạn tự vẽ :v
2) Phương trình hoành độ giao điểm của (d1) và (d2) là:
\(-\frac{1}{3}x+1\Leftrightarrow x+5\Leftrightarrow\frac{4}{3}x=-4\Leftrightarrow x=-3\Rightarrow y=x=5=-3+5=2\)
Vậy giao điểm của (d1) và (d2) có tọa độ là (-3;2)
3) Giả sử điểm A (2; -3m+1) thuộc (d1), ta có:
\(-3m+1=\frac{-1}{3}\cdot2+1\\ \Leftrightarrow-3m+1=-\frac{2}{3}+1\\ \Leftrightarrow-3m=-\frac{2}{3}\\ \Leftrightarrow m=\frac{2}{9}\)
Vậy với m = 2/9 thì điểm A thuộc (d1)

Tương tự như câu trước:
\(cos50^0=sin40^0< sin49^0< cot41^0=tan49^0< tan65^0< tan75^0=cot15^0\)