Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2: \(=\dfrac{\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)}{-\left(x-y\right)\left(x^2+xy+y^2\right)}=\dfrac{-\left(x+y\right)\left(x^2+y^2\right)}{x^2+xy+y^2}\)

\(x^2-9x+1=0\)
\(\Rightarrow\Delta=\left(-9\right)^2-4\cdot1\cdot1=77>0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{9+\sqrt{77}}{2}\\x_2=\dfrac{9-\sqrt{77}}{2}\end{matrix}\right.\)
Ta có:
\(V=x^4+x^2+\dfrac{1}{5}x^2=x^4+\dfrac{6}{5}x^2\)
Thay \(x_1,x_2\) vào V ta có:
\(V_1=\left(\dfrac{9+\sqrt{77}}{2}\right)^4+\dfrac{6}{5}\left(\dfrac{9+\sqrt{77}}{2}\right)^2\approx6333\)
\(V_2=\left(\dfrac{9-\sqrt{77}}{2}\right)^4+\dfrac{6}{5}\left(\dfrac{9-\sqrt{77}}{2}\right)^2\approx0,015\)

Bài 1:
$2xy=(x+y)^2-(x^2+y^2)=4^2-10=6\Rightarrow xy=3$
$M=x^6+y^6=(x^3+y^3)^2-2x^3y^3$
$=[(x+y)^3-3xy(x+y)]^2-2(xy)^3=(4^3-3.3.4)^2-2.3^3=730$
Bài 2:
$8x^3-32y-32x^2y+8x=0$
$\Leftrightarrow (8x^3+8x)-(32y+32x^2y)=0$
$\Leftrightarrow 8x(x^2+1)-32y(1+x^2)=0$
$\Leftrightarrow (8x-32y)(x^2+1)=0$
$\Rightarrow 8x-32y=0$ (do $x^2+1>0$ với mọi $x$)
$\Leftrightarrow x=4y$
Khi đó:
$M=\frac{3.4y+2y}{3.4y-2y}=\frac{14y}{10y}=\frac{14}{10}=\frac{7}{5}$

b: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow n\in\left\{0;-1;1\right\}\)

a) \(N=x^2-10x+25\)
\(N=x^2-2\cdot5\cdot x+5^2\)
\(N=\left(x-5\right)^2\)
Thay x = 55 vào N ta có:
\(N=\left(55-5\right)^2=2500\)
b) \(P=\dfrac{x^4}{4}-x^2y+y^2\)
\(P=\left(\dfrac{x^2}{2}\right)^2-2\cdot\dfrac{x^2}{2}\cdot y+y^2\)
\(P=\left(\dfrac{x^2}{2}-y\right)^2\)
Thay x = 4 và \(y=\dfrac{1}{2}\) vào P ta có:
\(P=\left(\dfrac{4^2}{2}-\dfrac{1}{2}\right)^2=\dfrac{225}{4}\)
Phần b mình thấy kết quả nó sai b ạ thầy cho mình đáp án là 225/9
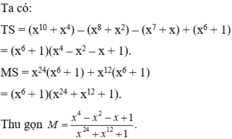

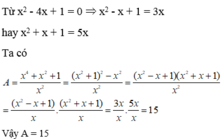

Xét \(x\ne1\)
Đặt \(y=x^4\).\(M=x^{28}+x^{24}+...+x^4+1\)
\(M=y^7+y^6+...+y^2+y+1\)\(\Rightarrow Ay=y^8+y^7+...+y^2+y\)
\(\Rightarrow M\left(y-1\right)=y^8-1\Rightarrow M=\frac{y^8-1}{y-1}=\frac{x^{32}-1}{x^4-1}\)
Tương tự \(N=x^{30}+x^{28}+...+x^2+1=\frac{\left(x^2\right)^{16}-1}{x-1}=\frac{x^{32}-1}{x-1}\)
\(A=\frac{M}{N}=\frac{\frac{x^{32}-1}{x^4-1}}{\frac{x^{32}-1}{x^2-1}}=\frac{x^2-1}{x^4-1}=\frac{1}{x^2+1}\)
Thay số vô tính ra A.