Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi BF,CE cắt nhau tại K và cắt AC,AB lần lượt tại S,T. Đường thẳng AH cắt MF,ME lần lượt tại P,Q.
Ta dễ thấy P là trực tâm của \(\Delta\)MAC, suy ra CP // EA (Cùng vuông góc AM). Tương tự BQ // FA
Áp dụng ĐL Melelaus và ĐL Thales ta có:
\(\frac{\overline{KB}}{\overline{KF}}.\frac{\overline{TA}}{\overline{TB}}.\frac{\overline{EF}}{\overline{EA}}=1\Rightarrow\frac{\overline{TA}}{\overline{TB}}=\frac{\overline{KF}}{\overline{KB}}.\frac{\overline{EA}}{\overline{EF}}=\frac{\overline{AF}}{\overline{QB}}.\frac{\overline{EA}}{\overline{EF}}\)
\(\frac{\overline{KC}}{\overline{KE}}.\frac{\overline{SA}}{\overline{SC}}.\frac{\overline{FE}}{\overline{FA}}=1\Rightarrow\frac{\overline{SC}}{\overline{SA}}=\frac{\overline{KC}}{\overline{KE}}.\frac{\overline{FE}}{\overline{FA}}=\frac{\overline{CP}}{\overline{EA}}.\frac{\overline{FE}}{\overline{FA}}\)
Suy ra \(\frac{\overline{TA}}{\overline{TB}}.\frac{\overline{HB}}{\overline{HC}}.\frac{\overline{SC}}{\overline{SA}}=\frac{\overline{CP}}{\overline{QB}}.\frac{\overline{HB}}{\overline{HC}}=-\frac{\overline{HC}}{\overline{HB}}.\frac{\overline{HB}}{\overline{HC}}=-1\)
Áp dụng điều kiện đủ của ĐL Ceva ta thu được AH,BS,CT đồng quy hay AH,BF,CE đồng quy (đpcm).

a, Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)
b, Vì AI là trung tuyến ứng ch BC nên \(AI=\dfrac{1}{2}BC=2,5\left(cm\right)\)
Áp dụng HTL: \(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12}{5}=2,4\left(cm\right)\)

a/ + Áp dụng hệ thức giữa cạnh và hình chiếu trong ΔΔABC vuông tại A có: AB2 = BC . BH => BH = AB2 : BC Hay BH = 92 : 15 => BH = 5,4 cm + Xét ΔΔABC vuông tại A có : HC = BC - BH Hay HC = 15 - 5,4 = 9,6 => HC = 9,6 cm + Áp dụng hệ thức liên quan đến đường cao trong ΔΔABC vuông tại A có : AH2 = BH . HC Hay AH2 = 5,4 . 9,6 AH2 = 51,84 => AH = √51,8451,84 = 7,2 cm
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=15^2-9^2=144\)
hay AC=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB\cdot AC=AH\cdot BC\)
\(\Leftrightarrow AH\cdot15=9\cdot12=108\)
hay AH=7,2(cm)
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=AH^2+CH^2\)
\(\Leftrightarrow CH^2=AC^2-AH^2=12^2-7.2^2=92.16\)
hay CH=9,6(cm)
Vậy: AH=7,2cm; CH=9,6cm

Ta có:
\(sinC=\dfrac{AB}{BC}\Rightarrow sin30^o=\dfrac{AB}{5}\)
\(\Rightarrow AB=5\cdot sin30^o=\dfrac{5}{2}\left(cm\right)\)
Mà: \(tanC=\dfrac{AB}{AC}\Rightarrow tan30^o=\dfrac{\dfrac{5}{2}}{AC}\)
\(\Rightarrow AC=\dfrac{\dfrac{5}{2}}{tan30^o}=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)
Theo hệ thức đường cao cạnh góc vuông và cạnh huyền ta có:
\(AB\cdot AC=AH\cdot BC\)
\(\Rightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{\dfrac{5}{2}\cdot\dfrac{5\sqrt{3}}{2}}{5}=\dfrac{5\sqrt{3}}{4}\left(cm\right)\)
Ta có: \(\left\{{}\begin{matrix}HB=\dfrac{AB^2}{BC}=\dfrac{\left(\dfrac{5}{2}\right)^2}{5}=\dfrac{5}{4}\left(cm\right)\\HC=\dfrac{AC^2}{BC}=\dfrac{\left(\dfrac{5\sqrt{3}}{2}\right)^2}{5}=\dfrac{15}{4}\left(cm\right)\end{matrix}\right.\)
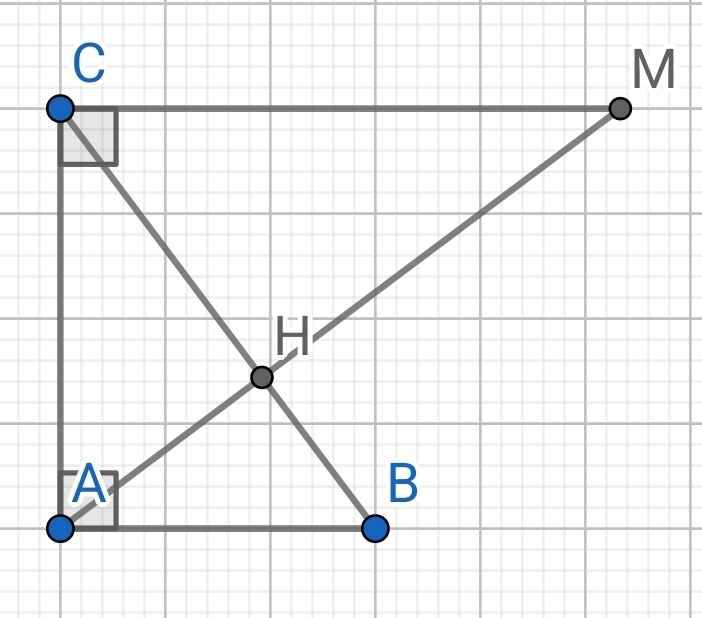 a) ∠ABC = 90⁰ - 30⁰ = 60⁰
a) ∠ABC = 90⁰ - 30⁰ = 60⁰
sinC = AB/BC
⇒ AB = BC.sinC
= 5.sin30⁰
= 5.1/2
= 5/2 (cm)
sinB = AC/BC
⇒ AC = BC.sinB
= 5.sin60⁰
= 5√3/2 (cm)
Ta có:
AH.BC = AB.AC
⇒ AH = AB.AC : BC
= 5/2 . 5√3/2 : 5
= 5√3/4 (cm)
AB² = BH.BC
⇒ BH = AB² : BC
= (5/2)² : 5
= 5/4 (cm)
⇒ CH = BC - BH
= 5 - 5/4
= 15/4 (cm)
b) Do AH ⊥ BC (gt)
⇒ CH ⊥ AM
∆ACM vuông tại C có CH là đường cao
⇒ AC² = AH . AM (1)
∆ABC vuông tại A có AH là đường cao
⇒ AC² = CH . CB (2)
Từ (1) và (2) ⇒ AH.AM = CH.CB

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{13^2-5^2}=12\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot13=5\cdot12=60\)
=>\(AH=\dfrac{60}{13}\left(cm\right)\)
Xét ΔAHB vuông tại H có
\(cosBAH=\dfrac{AH}{AB}=\dfrac{60}{13}:5=\dfrac{12}{13}\)
nên \(\widehat{BAH}\simeq23^0\)