Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Xét (O) có
ΔKAB nội tiếp đường tròn(K,A,B\(\in\)(O))
AB là đường kính
Do đó: ΔKAB vuông tại K(Định lí)
\(\Leftrightarrow\widehat{AKB}=90^0\)
hay \(\widehat{HKB}=90^0\)
Xét tứ giác BKHC có
\(\widehat{HKB}\) và \(\widehat{HCB}\) là hai góc đối
\(\widehat{HKB}+\widehat{HCB}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BKHC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay B,K,H,C cùng thuộc một đường tròn(đpcm)

a) Ta có AB và AC là tiếp tuyến tại A và B của (O)
=> AB⊥OB và AC⊥OC
Xét ΔAOB và ΔAOC có
OB=OC(=R)
Góc ABO=Góc ACO=90
OA chung
=> ΔAOB=ΔAOC
=> AB=AC
=> A∈trung trực của BC
Có OB=OC(=R)
=>O∈trung trực của BC
=> OA là đường trung trực của BC
Mà H là trung điểm của BC
=>A;H;O thẳng hàng
Xét ΔABO vuông tại B
=>A;B:O cùng thuộc đường tròn đường kính OA
Xét ΔACO vuông tại C
=>A;C;O cùng thuộc đuường tròn đường kính OA
=>A;B;C;O cùng thuộc đường tròn đường kính OA
b) Xét (O) có BD là đường kính
=>ΔBCD vuông tại C
=> CD⊥BC
Mà OA⊥BC
=>OA//CD
=> Góc AOC=Góc OCD
Xét ΔOCD có OC=OD
=> ΔOCD cân tại O
=> Góc OCD=Góc ODC
=> Góc ODC=Góc AOC
Xét ΔAOC và ΔCDK có
Góc AOC=Góc CDK
Góc ACO=Góc CKD=90
=>ΔAOC∞ΔCDK
=>AOCDAOCD= ACCKACCK
=>AC.CD=CK.OA
d) Xét ΔOCK vuông tại K
=> ΔOCK nội tiếp đường tròn đường kính OC
Xét ΔOHC vuông tại H
=> ΔOHC nội tiếp đường tròn đươngf kính OC
=> Tứ giác OKCH nội tiếp đường tròn đường kính OC
=> Góc CHK=Góc COD
Có góc BOA=Góc BCK( cùng phụ góc CBD)
Góc CHI+góc BCK=Góc BOA+ góc BAO
=>Góc CHI=Góc BAO
Mà Góc BAO=Góc CBD( cùng phụ góc ABC)
=> Góc CHI=Góc CBD
=> HI//BD
Xét ΔBCD có HI//BD và H là trung điểm của BC
=> HI là đường trung bình của ΔBCD
=> I là trung điểm của CK

3 căn 3/5 nhé
nếu cần trình bày thì bn kẻ hình ra
rồi có ob=oa=oc
ad đl pytago cho tam giác vuoong nnhes

a) Bán kính OA vuông góc với BC nên MB = MC.
Lại có MO = MA ( gt )
Suy ra tứ giác OBAC là hình bình hành vì có các đường chéo cắt nhau tại trung điểm mỗi đường.
Lại có: OA \(\perp\) BC nên OBAC là hình thoi.
b) Ta có: OA = OB (bán kính)
OB = BA (tính chất hình thoi).
Nên OA = OB = BA => \(\Delta AOB\)đều => ∠AOB = 60o
Trong tam giác OBE vuông tại B ta có:
BE = OB . tg∠AOB = OB . tg60o = \(R.\sqrt{3}\)

Gọi I là trung điểm của AB
Suy ra: IO = IA = (1/2).OA = 3/2
Ta có: BC ⊥ OA (gt)
Suy ra: góc (OIB) = 90 °
Áp dụng định lí Pitago vào tam giác vuông OBI ta có: O B 2 = B I 2 + I O 2
Suy ra: B I 2 = O B 2 - I O 2
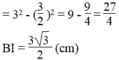
Ta có: BI = CI (đường kính dây cung)
![]()
- Gọi I là giao điểm của BC và OC
( IO = IA = 1,5cm ) ( OB = OA = 3cm )
Áp dụng đlí Py - ta - go cho tam giác vuông IBO ( ^I = 90^o ) , ta có :
\(OB^2=IB^2+IO^2\)
\(3^2=IB^2+1,5^2\)
\(IB^2=3^2-1,5^2=9-2,25=6,75\)
\(\Rightarrow IB=\sqrt{6,75}\approx2,6\)
Mà \(OA\perp BC\Rightarrow IC=IB\)( t/c đường kính vuông với dây cung )
=> BC = 2 . IB = 2 . 2,6 = 5,2
Vậy : BC = 5,2cm
Gọi giao điểm của MN với OA là H
Vì MN\(\perp\)OA tại trung điểm của OA
nên MN\(\perp\)OA tại H và H là trung điểm của OA
Xét ΔOMA có
MH là đường cao
MH là đường trung tuyến
Do đó: ΔOMA cân tại M
=>MO=MA
mà OM=OA
nên OM=MA=OA
=>ΔOMA đều
=>\(\widehat{MOA}=60^0\)
Xét ΔMHO vuông tại H có \(sinMOH=\dfrac{MH}{MO}\)
=>\(\dfrac{MH}{10}=sin60=\dfrac{\sqrt{3}}{2}\)
=>\(MH=10\cdot\dfrac{\sqrt{3}}{2}=5\sqrt{3}\left(cm\right)\)
ΔOMN cân tại O
mà OH là đường cao
nên H là trung điểm của MN
=>\(MN=2\cdot MH=2\cdot5\sqrt{3}=10\sqrt{3}\left(cm\right)\)