NH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
23 tháng 12 2019
Đáp án A
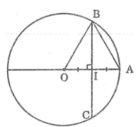
Gọi H là trung điểm của BC.
Do dây BC vuông góc với OA tại H nên ta có:
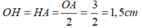
Áp dụng định lí Pytgo vào tam giác OHB vuông tại H ta có:
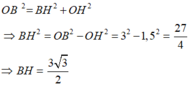
Theo định lí quan hệ vuông góc đường kính và dây ta có: H là trung điểm BC nên:
8 tháng 12 2021
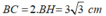
3 căn 3/5 nhé
nếu cần trình bày thì bn kẻ hình ra
rồi có ob=oa=oc
ad đl pytago cho tam giác vuoong nnhes
CM
14 tháng 2 2018
Gọi I là trung điểm của AB
Suy ra: IO = IA = (1/2).OA = 3/2
Ta có: BC ⊥ OA (gt)
Suy ra: góc (OIB) = 90 °
Áp dụng định lí Pitago vào tam giác vuông OBI ta có: O B 2 = B I 2 + I O 2
Suy ra: B I 2 = O B 2 - I O 2
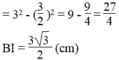
Ta có: BI = CI (đường kính dây cung)
HH
20 tháng 1 2021
- Gọi I là giao điểm của BC và OC
( IO = IA = 1,5cm ) ( OB = OA = 3cm )
Áp dụng đlí Py - ta - go cho tam giác vuông IBO ( ^I = 90^o ) , ta có :
\(OB^2=IB^2+IO^2\)
\(3^2=IB^2+1,5^2\)
\(IB^2=3^2-1,5^2=9-2,25=6,75\)
\(\Rightarrow IB=\sqrt{6,75}\approx2,6\)
Mà \(OA\perp BC\Rightarrow IC=IB\)( t/c đường kính vuông với dây cung )
=> BC = 2 . IB = 2 . 2,6 = 5,2
Vậy : BC = 5,2cm
31 tháng 12 2021
a: Sửa đề: CM BN//OD
Xét (O) có
ΔBNC nội tiếp
CN là đường kính
Do đó: ΔBNC vuông tại B(1)
Xét (O) có
DB là tiếp tuyến
DC là tiếp tuyến
Do đó: DB=DC
hay D nằm trên đường trung trực của BC(2)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(3)
Từ (2) và (3) suy ra OD⊥BC(4)
Từ (1) và (4) suy ra BN//OD
27 tháng 12 2019
a) Ta có AB và AC là tiếp tuyến tại A và B của (O)
=> AB⊥OB và AC⊥OC
Xét ΔAOB và ΔAOC có
OB=OC(=R)
Góc ABO=Góc ACO=90
OA chung
=> ΔAOB=ΔAOC
=> AB=AC
=> A∈trung trực của BC
Có OB=OC(=R)
=>O∈trung trực của BC
=> OA là đường trung trực của BC
Mà H là trung điểm của BC
=>A;H;O thẳng hàng
Xét ΔABO vuông tại B
=>A;B:O cùng thuộc đường tròn đường kính OA
Xét ΔACO vuông tại C
=>A;C;O cùng thuộc đuường tròn đường kính OA
=>A;B;C;O cùng thuộc đường tròn đường kính OA
b) Xét (O) có BD là đường kính
=>ΔBCD vuông tại C
=> CD⊥BC
Mà OA⊥BC
=>OA//CD
=> Góc AOC=Góc OCD
Xét ΔOCD có OC=OD
=> ΔOCD cân tại O
=> Góc OCD=Góc ODC
=> Góc ODC=Góc AOC
Xét ΔAOC và ΔCDK có
Góc AOC=Góc CDK
Góc ACO=Góc CKD=90
=>ΔAOC∞ΔCDK
=>AOCDAOCD= ACCKACCK
=>AC.CD=CK.OA
d) Xét ΔOCK vuông tại K
=> ΔOCK nội tiếp đường tròn đường kính OC
Xét ΔOHC vuông tại H
=> ΔOHC nội tiếp đường tròn đươngf kính OC
=> Tứ giác OKCH nội tiếp đường tròn đường kính OC
=> Góc CHK=Góc COD
Có góc BOA=Góc BCK( cùng phụ góc CBD)
Góc CHI+góc BCK=Góc BOA+ góc BAO
=>Góc CHI=Góc BAO
Mà Góc BAO=Góc CBD( cùng phụ góc ABC)
=> Góc CHI=Góc CBD
=> HI//BD
Xét ΔBCD có HI//BD và H là trung điểm của BC
=> HI là đường trung bình của ΔBCD
=> I là trung điểm của CK
2 tháng 11 2017
Ta có BC ⊥ OA ⇒ BE = EC
E là trung điểm của OA ⇒ OE = AE và OA=OB= 3cm
OE=\(\dfrac{OA}{2}\) =\(\dfrac{3}{2}\) = 1.5 cm
ΔHBO vuông tại E :
BE=\(\sqrt{OB^2-OE^2}\)
=\(\sqrt{3^2-1.5^2}\) =\(\dfrac{3\sqrt{3}}{2}\) cm
⇒ BC= 2BE
= 2. \(\dfrac{3\sqrt{3}}{2}\) = \(3\sqrt{3}\) cm
16 tháng 10 2021
a, Xét tam giác MON có : OM = ON = R
=> tam giác MON cân tại O, do OI vuông MN hay OI là đường cao
đồng thời là đường phân giác => ^MOI = ^ION
Vì BN là tiếp tuyến đường tròn (O) với N là tiếp điểm
=> ON vuông BN hay ^ONB = 900
Xét tam giác IOM và tam giác NOB có :
^IOM = ^NOB ( cmt )
^OIM = ^ONB = 900
Vậy tam giác IOM ~ tam giác NOB ( g.g )
=> \(\frac{IO}{NO}=\frac{IM}{NB}\Rightarrow IO.NB=IM.NO\)
ý b sáng mai mình gửi nhé ;))
16 tháng 10 2021
sửa hộ mình chỗ này nhé : ^OIM = ^ONB = 900
b, Vì I là trung điểm điểm OA => \(IO=IA=\frac{OA}{2}=\frac{R}{2}\)
Theo định lí Pytago tam giác OIM ta được :
\(MI=\sqrt{OM^2-OI^2}=\sqrt{R^2-\frac{R^2}{4}}=\sqrt{\frac{3R^2}{4}}=\frac{\sqrt{3}R}{2}\)
Vì BM là tiếp tuyến đường tròn (O) và M là tiếp điểm
=> OM vuông MB hay ^OMB = 900 => tam giác OMB vuông tại M
Xét tam giác OMB vuông tại M, đường cao MI
Áp dụng hệ thức : \(\frac{1}{OM^2}+\frac{1}{MB^2}=\frac{1}{MI^2}\Rightarrow\frac{1}{R^2}+\frac{1}{MB^2}=\frac{1}{\frac{3R^2}{4}}\)
\(\Leftrightarrow\frac{1}{R^2}+\frac{1}{MB^2}=\frac{4}{3R^2}\Leftrightarrow\frac{1}{MB^2}=\frac{4}{3R^2}-\frac{1}{R^2}=\frac{1}{3R^2}\Rightarrow MB=\sqrt{3}R\)
CM : tam giác OMB = tam giác ONB ( ch - gn )
Ta có : \(S_{OMNB}=S_{OMB}+S_{ONB}=2S_{OMB}=\frac{2.1}{2}.OM.MB\)
\(=R.\sqrt{3}R=\sqrt{3}R^2\)
5 cm nha .