Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
- Điện trở của dây nhôm là:
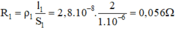
- Điện trở của dây nikêlin là:
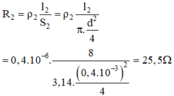
- Điện trở của dây đồng là:
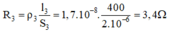
Điện trở dây:
\(R=\rho\cdot\dfrac{l}{S}=1,1\cdot10^{-6}\cdot\dfrac{62,8}{\pi\cdot\dfrac{d^2}{4}}=1,1\cdot10^{-6}\cdot\dfrac{62,8}{\pi\cdot\dfrac{(2\cdot10^{-3})^2}{4}}\approx22\Omega\)
Dòng điện qua dây:
\(I=\dfrac{U}{R}=\dfrac{110}{22}=5A\)
`*` Tóm tắt:
\(R=110\Omega\\ U=220V\\ \rho=1,10\cdot10^{-6}\Omega\cdot m\\ l=6,8m\\ ------------\\ a,I=?A\\ b,S=?m^2\)
_
`*` Giải:
`a,` Cường độ dòng điện chạy qua bếp:
\(I=\dfrac{U}{R}=\dfrac{220}{110}=2A\)
`b,` Tiết diện của dây:
\(R=\dfrac{\rho\cdot l}{S}\Rightarrow S=\dfrac{\rho\cdot l}{R}=\dfrac{1,10\cdot10^{-6}\cdot6,8}{110}=0,068\cdot10^{-6}m^2.\)
Câu 2:
a,\(R_{tđ}=R_1+R_{bt}\Rightarrow R_{bt}=R_{tđ}-R_1=\dfrac{U}{I}-R_1=\dfrac{6}{0,5}-10=2\left(\Omega\right)\)
Vì R1 nối tiếp với Rbt nên Itoàn mạch = I1 = Ibt = 0,5A
b,Công suất tiêu thụ của biến trở: \(P_{bt}=I^2R=0,5^2.2=0,5\left(W\right)\)
Công suất tiêu thụ của toàn mạch: \(P_{tm}=UI=6.0,5=3\left(W\right)\)
c, Đổi: 20p= 1200s
Điện năng tiêu thụ của đoạn mạch trong 20p: \(Q=P.t=3.1200=3600\left(J\right)\)
Qua bảng 1 ta tra được điện trở suất của dây constantan là ρ = 0,50.10-6 Ω.m
Có nghĩa là nếu ta có một sợi dây constantan hình trụ có chiều dài l1 = 1m, tiết diện S1 = 1m2 thì điện trở của nó là: R1 = 0,50.10-6Ω
→ Điện trở của đoạn dây dẫn constantan dài l = l m = l1 và có tiết diện S = l mm2 là R thỏa mãn hệ thức
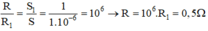
\(R1=p1\dfrac{l1}{S1}\Rightarrow p1=\dfrac{R1\cdot S1}{l1}=\dfrac{12\cdot1\cdot10^{-6}}{200}=6\cdot10^{-8}\Omega m\)
Vì hai dây dẫn này cùng chất nên p1 = p2.
\(R2=p2\dfrac{l2}{S2}\Rightarrow l2=\dfrac{R2\cdot S2}{p2}=\dfrac{24\cdot2\cdot10^{-6}}{6\cdot10^{-8}}=800m\)
Chọn D
Lập tỉ lệ ta dc
\(\dfrac{R_1}{R_2}=\dfrac{\rho\dfrac{l_1}{S_1}}{\rho\dfrac{l_2}{S_2}}\Rightarrow\dfrac{12}{24}=\dfrac{\dfrac{200}{1\cdot10^{-6}}}{\dfrac{l_2}{2\cdot10^{-6}}}\Rightarrow l_2=800\left(m\right)\)
chọn D
+)Điện trở của biến trở là:\(R_B=\rho.\dfrac{l}{S}=1,1.10^{-6}.\dfrac{4}{1.10^{-7}}=44\left(ÔM\right)\) (đổi \(0,1mm^2=1.10^{-7}m^2\))
+)
Cường độ dòng điện lúc biến trở có giá trị lớn nhất:
\(I_B=\dfrac{U}{R_{TĐ}}=\dfrac{30}{44+20}=0,47\left(A\right)\)
Cường độ dòng điện lúc biến trở nhỏ nhất:
\(I_B=\dfrac{U}{R_{TĐ}}=\dfrac{30}{0+20}=1,5\left(A\right)\)
Vậy cường độ dòng điện có thể thay đổi từ: \(0,47A\rightarrow1,5A\)
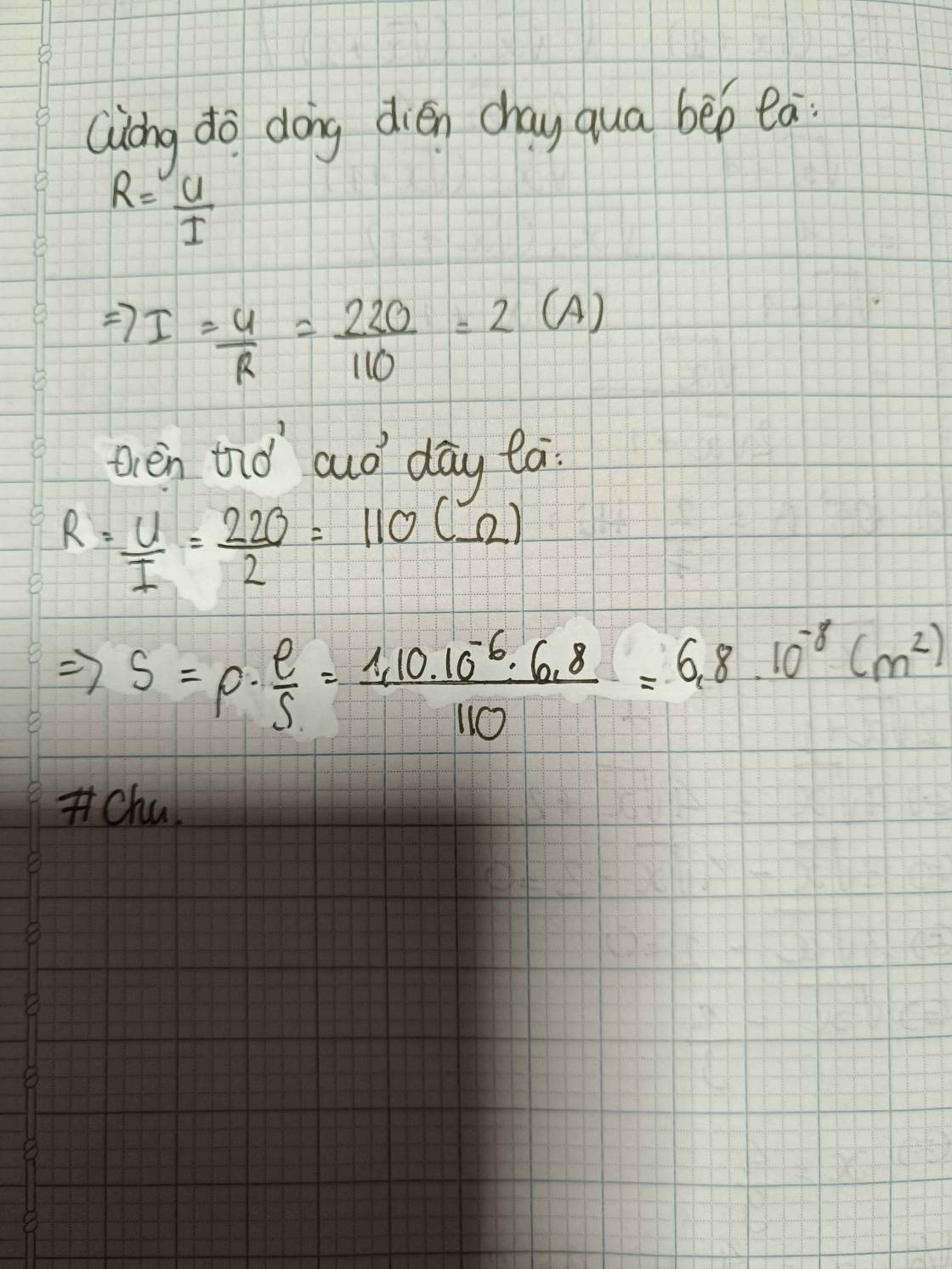
Điện trở của dây nicrom: \(R=p\dfrac{l}{S}=1,10.10^{-6}\dfrac{1}{1.10^{-6}}=1,1\Omega\)