Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

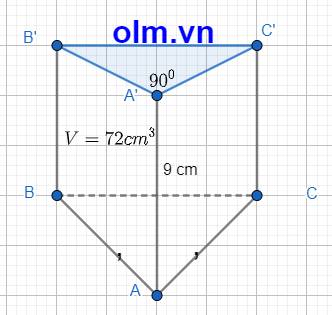
VABCA'B'C' = SABC.h
Diện tích của tam giác ABC là: 72 : 9 = 8 (cm2)
SABC = \(\dfrac{1}{2}\)AB.AC = \(\dfrac{1}{2}\)AB2 = 8 ⇒ AB2 = 8.2 = 16
⇒ AB = AC = \(\sqrt{16}\) = 4 (cm)
Vậy độ dài cạnh đáy AB dài 4cm

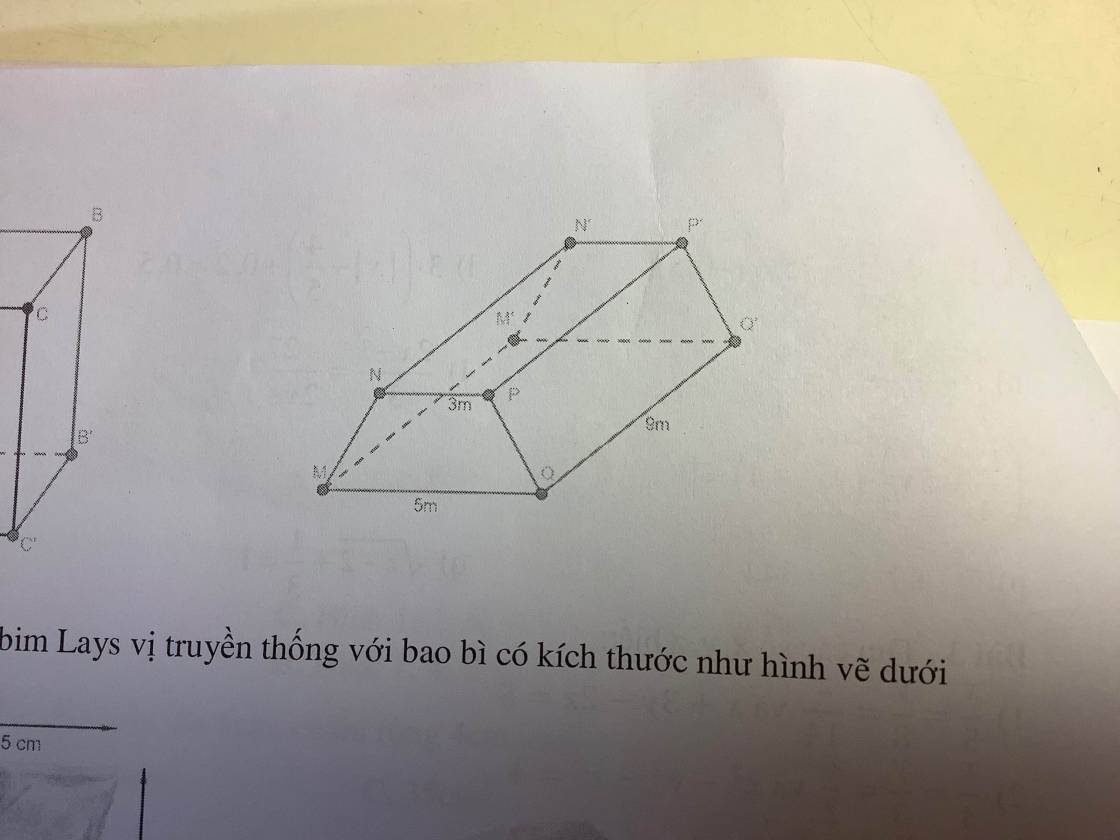
Chu vi đáy là 3+4+5=12(cm)
Diện tích xung quanh của hình trụ là:
\(S_{xq}=12\cdot7=84\left(cm^2\right)\)
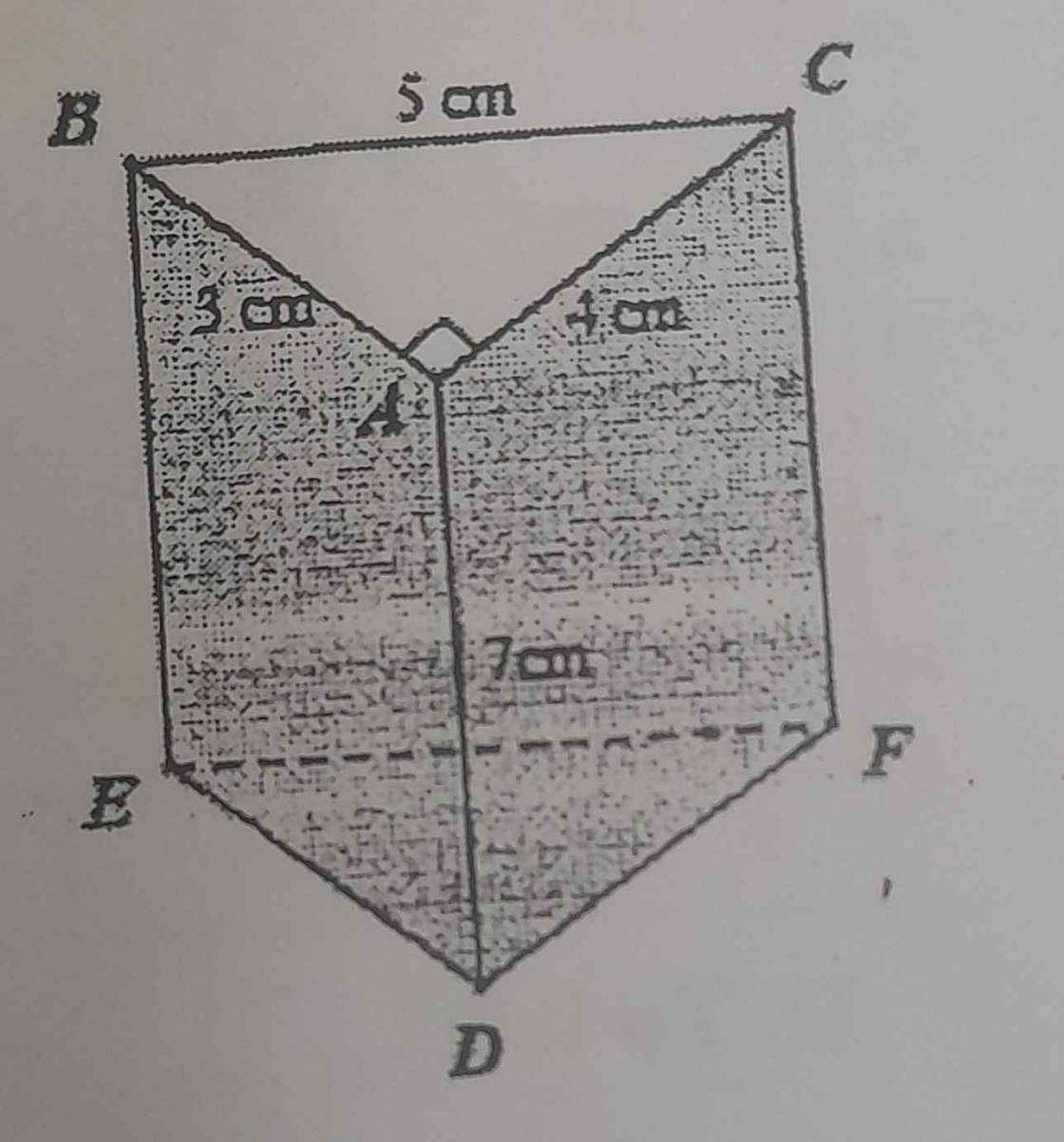
Vì \(AB^2+AC^2=BC^2\)
nên ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)\)
Thể tích của lăng trụ là:
\(V=S_{đáy}\cdot cao=6\cdot7=42\left(cm^3\right)\)

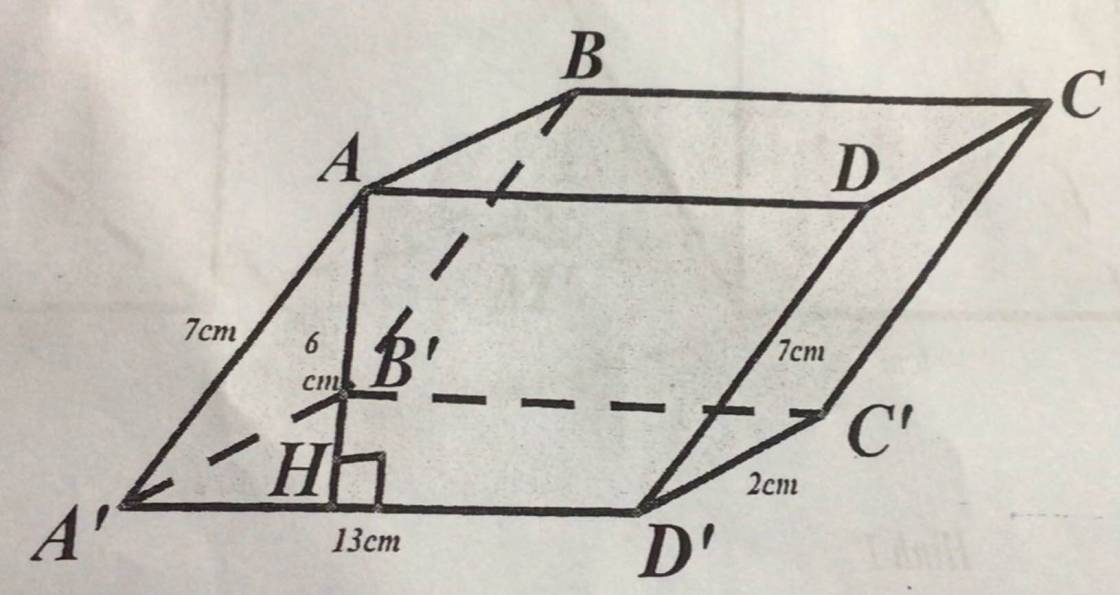
Ta có Sxq= chu vi đáy (hình bình hành) nhân chiều cao= 2.(7+13).2=80 cm vuông
Ta có V(thể tích)= S đáy . Chiều cao=6.13.2=156 cm khối
Chúc bạn học tốt và nhớ đọc kỹ kiến thức trong sách giáo khoa

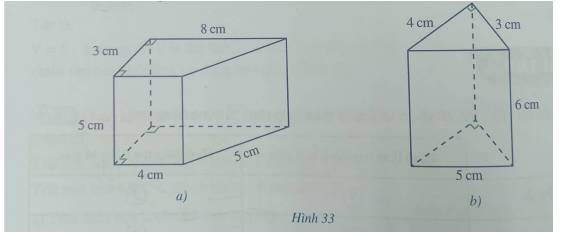
i) Hình 33b là hình lăng trụ đứng tam giác
Hình 33a là hình lăng trụ đứng tứ giác
ii) Hình 33a: Sxq = (3+4+5+8).5 = 100 (cm2)
Hình 33b: Sxq = (3+4+5).6 = 72 (cm2)
iii) Hình 33a: Diện tích đáy là: (8+4).3:2=18 (cm2)
Thể tích là: V = 18.5 = 90 (cm3)
Hình 33b: Diện tích đáy là: \(\dfrac{1}{2}3.4=6\) (cm2)
Thể tích là: V= 6.6=36 (cm3)

Diện tích xung quanh lăng trụ là :
\(\left(10+2+2.5\right).5=110\left(m^2\right)\)
Diện tích toàn phần lăng trụ là :
\(110+2.\left(10+2\right).3.\dfrac{1}{2}=146\left(m^2\right)\)
Đáp số...
Diện tích xung quanh hình lăng trụ tứ giá đều ABCDA'B'C'D' là
Áp dụng ct :Sxq = 2.p.h
Sxq= 2.2.5.10 = 200 (cm2)
Thể tích của hình lăng trụ tứ giác đều ABCDA'B'C'D' là :
Áp Dụng công thức V = S.h
V = 5.5.10 = 250 (cm3)
Kết luận :..........