Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 Giải
Chu vi HCN là:
(12+8).2= 40(cm)
Diện tích HCN là:
12.8= 96(cm)
Bài 2 Chu vi hình vuông là:
20.4=80(cm)
Mà chu vi hình vuông bằng chu vi HCN nên:
Chiều rộng HCN là:
(80:2) -25=15(cm)
Diện tích HCN là:
15.25=375(cm)
Bài 3 Độ dài cạnh BC là:
120:10.2=24(cm)
Bài 4 Diện tích tam giác ABC là:
( 5.8):2 = 20(cm)
Chúc bn hok tốt~~

1/ Gọi chiều dài hình chữ nhật đó là x ( cm , x > 5 )
=> Chiều rộng hình chữ nhật đó là x - 5 ( cm )
Theo đề bài ta có : x( x - 5 ) = 300
<=> x2 - 5x - 300 = 0
<=> x2 + 15x - 20x - 300 = 0
<=> x( x + 15 ) - 20( x + 15 ) = 0
<=> ( x + 15 )( x - 20 ) = 0
<=> x = -15 ( không tmđk ) hoặc x = 20 ( tmđk )
=> Chiều dài hình chữ nhật là 20cm
Chiều rộng hình chữ nhật là 20 - 5 = 15cm
Chu vi hình chữ nhật đó là : 2( 20 + 15 ) = 70cm
2/ Gọi độ dài cạnh góc vuông lớn là x( cm , x > 1 )
=> Độ dài cạnh góc vuông nhỏ là x - 1
Theo định lý Pytago ta có :
x2 + ( x - 1 )2 = 52
<=> x2 + x2 - 2x + 1 = 25
<=> 2x2 - 2x + 1 - 25 = 0
<=> 2x2 - 2x - 24 = 0
<=> 2( x2 - x - 12 ) = 0
<=> x2 - x - 12 = 0
<=> x2 + 3x - 4x - 12 = 0
<=> x( x + 3 ) - 4( x + 3 ) = 0
<=> ( x - 4 )( x + 3 ) = 0
<=> x = 4 ( tmđk ) hoặc x = -3 ( không tmđk )
=> Độ dài cạnh góc vuông lớn là 4cm
=> Độ dài cạnh góc vuông bé là 4 - 1 = 3cm
Chu vi hình tam giác = 3 + 4 + 5 = 12cm
1) Gọi chiều dài của hình chữ nhật là \(a\left(a>0,cm\right)\)
Chiều rộng của hình chữ nhật là : \(a-5\left(cm\right)\)
Thoe bài ta có : \(a.\left(a-5\right)=300\Leftrightarrow\left(a-20\right)\left(a+15\right)=0\)
\(\Leftrightarrow a=20\left(a>0\right)\)( Thỏa mãn )
Chiều rộng hình chữ nhật là : \(a-5=15\left(cm\right)\)
Vậy chu vi HCN đó là : \(\left(20+15\right)\cdot2=70\left(cm\right)\)
2) Gọi cạnh góc vuông lớn hơn là \(x\left(x>0,cm\right)\)
Cạnh góc vuông nhỏ hơn là : \(x-1\left(cm\right)\)
Theod dịnh lý Pytago thì : \(x^2+\left(x-1\right)^2=5^2\)
\(\Leftrightarrow2x^2-2x-24=0\)
\(\Leftrightarrow x^2-x-12=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+3\right)=0\)
\(\Leftrightarrow x=4\left(x>0\right)\) ( Thỏa mãn )
Vậy cạnh góc vuông còn lại là \(x-1=3\left(cm\right)\)
Chu vi tam giác đó là : \(3+4+5=12\left(cm\right)\)

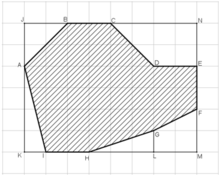
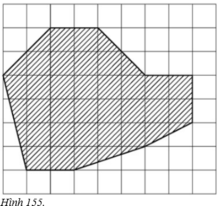
Diện tích hình chữ nhật JKMN là: 8.6 = 48 (cm2)
Diện tích tam giác vuông JAB là: JA.JB/2 = 2.2/2 = 2 (cm2).
Diện tích tam giác vuông AKI là: AK.KI/2 = 2 (cm2).
Diện tích tam giác vuông HLG là: HL.LG/2 = 1,5 (cm2).
Diện tích hình thang vuông GLMF là:
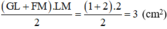
Diện tích hình thang vuông CDEN là:
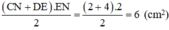
Vậy diện tích của hồ nước trên bản đồ là:
SABCDEFGHI = SJKML – SAJB – SAKI – SHLG – SGLMF – SCDEN
= 48 – 2 – 2 – 1,5 – 3 – 6
= 33,5 (cm2).
Bản đồ tỉ lệ 1 : 10 000 nên diện tích thực của hồ là:
33,5.(10000)2 = 33,5.108 (cm2) = 33,5 (ha)
(Lưu ý: tỉ lệ 1 : 10 000 tức là 1cm trên bản đồ ứng với 10 000cm trên thực tế. Suy ra, 1cm2 trên bản đồ ứng với (10 000)2 cm2 trên thực tế)

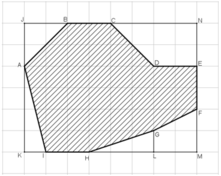
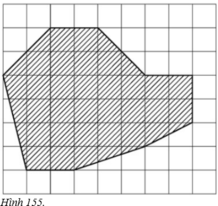
Diện tích hình chữ nhật JKMN là: 8.6 = 48 (cm2)
Diện tích tam giác vuông JAB là: JA.JB/2 = 2.2/2 = 2 (cm2).
Diện tích tam giác vuông AKI là: AK.KI/2 = 2 (cm2).
Diện tích tam giác vuông HLG là: HL.LG/2 = 1,5 (cm2).
Diện tích hình thang vuông GLMF là:
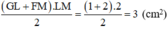
Diện tích hình thang vuông CDEN là:
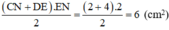
Vậy diện tích của hồ nước trên bản đồ là:
SABCDEFGHI = SJKML – SAJB – SAKI – SHLG – SGLMF – SCDEN
= 48 – 2 – 2 – 1,5 – 3 – 6
= 33,5 (cm2).
Bản đồ tỉ lệ 1 : 10 000 nên diện tích thực của hồ là:
33,5.10 000 = 335 000 (cm2) = 33,5 m2.

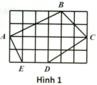
Đoạn thẳng \(AB\) là đường chéo của hình chữ nhật với chiều dài là \(4cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(A{B^2} = {2^2} + {4^2} = 4 + 16 = 20 \Rightarrow AB = \sqrt {20} = 2\sqrt 5 \)
Đoạn thẳng \(AC\) là đường chéo của hình chữ nhật với chiều dài là \(4cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(A{C^2} = {2^2} + {4^2} = 4 + 16 = 20 \Rightarrow AC = \sqrt {20} = 2\sqrt 5 \)
Đoạn thẳng \(BC\) là đường chéo của hình chữ nhật với chiều dài là \(6cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(B{C^2} = {2^2} + {6^2} = 4 + 36 = 40 \Rightarrow BC = \sqrt {40} = 2\sqrt {10} \)
Từ hình vẽ ta thấy:
\(Q\) là trung điểm của \(AC\);
\(R\) là trung điểm của \(AB\);
\(P\) là trung điểm của \(BC\).
- Vì \(Q\) là trung điểm của \(AC\); \(R\) là trung điểm của \(AB\) nên \(QR\) là đường trung bình của tam giác \(ABC \Rightarrow QR = \frac{1}{2}BC\) (tính chất đường trung bình)
\( \Leftrightarrow QR = \frac{1}{2}.2\sqrt {10} = \sqrt {10} \left( {cm} \right)\).
- Vì \(Q\) là trung điểm của \(AC\); \(P\) là trung điểm của \(BC\) nên \(QP\) là đường trung bình của tam giác \(ABC \Rightarrow QP = \frac{1}{2}AB\) (tính chất đường trung bình)
\( \Leftrightarrow QP = \frac{1}{2}.2\sqrt 5 = \sqrt 5 \left( {cm} \right)\).
- \(R\) là trung điểm của \(AB\); \(P\) là trung điểm của \(BC\) nên \(RP\) là đường trung bình của tam giác \(ABC \Rightarrow RP = \frac{1}{2}AC\) (tính chất đường trung bình)
\( \Leftrightarrow RP = \frac{1}{2}.2\sqrt 5 = \sqrt 5 \left( {cm} \right)\).
\(AB=\sqrt{4^2+2^2}=2\sqrt{5}\left(cm\right);AC=\sqrt{4^2+2^2}=2\sqrt{5}\left(cm\right)\)
BC=căn 2^2+6^2=2*căn 10(cm)
Xét ΔABC có P,Q lần lượt là trung điểm của CB,CA
=>PQ là đường trung bình
=>\(PQ=\dfrac{AB}{2}=\sqrt{5}\left(cm\right)\)
Xét ΔABCcóQ,R lần lượt là trung điểm của AC,AB
=>QR là đường trung bình
=>\(QR=\dfrac{BC}{2}=\sqrt{10}\left(cm\right)\)
Xét ΔABC có P,R lần lượt là trung điểm của BC,BA
=>PR là đường trung bình
=>\(PR=\dfrac{AC}{2}=\sqrt{5}\left(cm\right)\)

Xét ΔBAC vuông tại A có tan ABC=AC/AB
=>1/AB=tan 30
=>\(AB=\sqrt{3}\left(cm\right)\)
=>\(S_{ABC}=\dfrac{\sqrt{3}}{2}\left(cm^2\right)\)
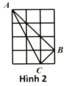
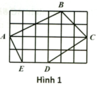

SABC = 3cm2