Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xin lỗi bn mink mới học có lớp 5 thôi à nên MINK ko thể giúp bn, xin lỗi nha

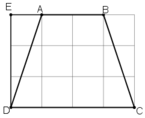
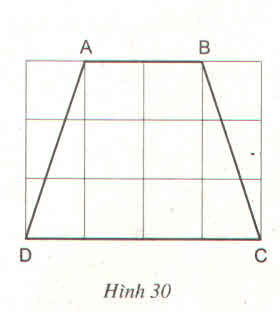
(Mỗi ô vuông là 1cm).
Nhìn vào hình vẽ ta thấy :
+ AB = 2cm
+ CD = 4cm.
+ Tính AD :
Xét tam giác vuông ADE có AE = 1cm, DE = 3cm.
⇒ AD2 = AE2 + DE2 (Định lý Pytago)
= 12 + 32 = 10
⇒ AD = √10 cm
+ Tính BC :
ABCD là hình thang cân nên BC = AD = √10 cm.
Vậy AB = 2cm, CD = 4cm, AD = BC = √10 cm.

Bài giải:
Theo hình vẽ, ta có: AB = 2cm, CD = 4cm
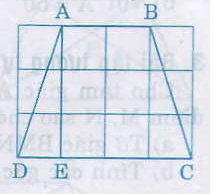
Trong tam giác vuông AED, áp dụng định lý Pitago ta được:
AD2 = AE2 + ED2
= 32 + 12 =10
Suy ra AD = cm
Vậy AB = 2cm, CD = 4cm, AD = BC = cm
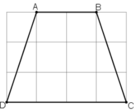
Áp dụng định lí Pitago :
\(AD^2 = AH^2 + DH^2\)
\(= 3^2 + 1^2\)
\(= 10\)
\(\Rightarrow AD=\sqrt{10}\)
Vậy \(AB = 2cm\);\(CD = 4cm\);\(AD=BC=\sqrt{10}\)

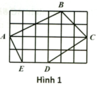
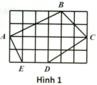
Đoạn thẳng \(AB\) là đường chéo của hình chữ nhật với chiều dài là \(4cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(A{B^2} = {2^2} + {4^2} = 4 + 16 = 20 \Rightarrow AB = \sqrt {20} = 2\sqrt 5 \)
Đoạn thẳng \(AC\) là đường chéo của hình chữ nhật với chiều dài là \(4cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(A{C^2} = {2^2} + {4^2} = 4 + 16 = 20 \Rightarrow AC = \sqrt {20} = 2\sqrt 5 \)
Đoạn thẳng \(BC\) là đường chéo của hình chữ nhật với chiều dài là \(6cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(B{C^2} = {2^2} + {6^2} = 4 + 36 = 40 \Rightarrow BC = \sqrt {40} = 2\sqrt {10} \)
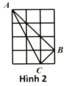
Từ hình vẽ ta thấy:
\(Q\) là trung điểm của \(AC\);
\(R\) là trung điểm của \(AB\);
\(P\) là trung điểm của \(BC\).
- Vì \(Q\) là trung điểm của \(AC\); \(R\) là trung điểm của \(AB\) nên \(QR\) là đường trung bình của tam giác \(ABC \Rightarrow QR = \frac{1}{2}BC\) (tính chất đường trung bình)
\( \Leftrightarrow QR = \frac{1}{2}.2\sqrt {10} = \sqrt {10} \left( {cm} \right)\).
- Vì \(Q\) là trung điểm của \(AC\); \(P\) là trung điểm của \(BC\) nên \(QP\) là đường trung bình của tam giác \(ABC \Rightarrow QP = \frac{1}{2}AB\) (tính chất đường trung bình)
\( \Leftrightarrow QP = \frac{1}{2}.2\sqrt 5 = \sqrt 5 \left( {cm} \right)\).
- \(R\) là trung điểm của \(AB\); \(P\) là trung điểm của \(BC\) nên \(RP\) là đường trung bình của tam giác \(ABC \Rightarrow RP = \frac{1}{2}AC\) (tính chất đường trung bình)
\( \Leftrightarrow RP = \frac{1}{2}.2\sqrt 5 = \sqrt 5 \left( {cm} \right)\).
\(AB=\sqrt{4^2+2^2}=2\sqrt{5}\left(cm\right);AC=\sqrt{4^2+2^2}=2\sqrt{5}\left(cm\right)\)
BC=căn 2^2+6^2=2*căn 10(cm)
Xét ΔABC có P,Q lần lượt là trung điểm của CB,CA
=>PQ là đường trung bình
=>\(PQ=\dfrac{AB}{2}=\sqrt{5}\left(cm\right)\)
Xét ΔABCcóQ,R lần lượt là trung điểm của AC,AB
=>QR là đường trung bình
=>\(QR=\dfrac{BC}{2}=\sqrt{10}\left(cm\right)\)
Xét ΔABC có P,R lần lượt là trung điểm của BC,BA
=>PR là đường trung bình
=>\(PR=\dfrac{AC}{2}=\sqrt{5}\left(cm\right)\)