Tính Δ y và ∆ y ∆ x của các hàm số sau theo x và Δ x : ...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

30 tháng 7 2019

Tính Δ y và ∆ y ∆ x của các hàm số sau theo x và Δ x : y = x 2 - 1

#Toán lớp 11

Cao Minh Tâm

30 tháng 7 2019

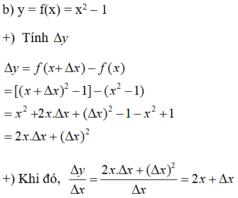
Giải bài tập Toán 11 | Giải Toán lớp 11

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Pham Trong Bach

9 tháng 4 2019

Cho hàm số có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 và tiếp xúc với (H) thì phương trình của Δ là A. y = x + 4. D. Không tồn...

Đọc tiếp

#Toán lớp 11

Cao Minh Tâm

9 tháng 4 2019

Chọn C.

Đạo hàm: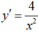

Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 nên có hệ số góc bằng 1.

Ta có phương trình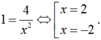

Tại M(2; 0). Phương trình tiếp tuyến là y = x – 2.

Tại N(-2; 4). Phương trình tiếp tuyến là y = x + 6.

Đúng(0)

Trinh Quynh Nhi

21 tháng 2 2022

Trong mặt phẳng với hệ tọa độ Oxy. Phép tịnh tiến theo vectơ biến đường thẳng Δ: x - y -1 = 0 thành đường thẳng Δ' có phương trình làA.x - y - 1 = 0 .B. x + y - 1 = 0 .C. x - y - 2 = 0 .D. x + y + 2 = 0...

Đọc tiếp

#Toán lớp 11

Nguyễn Lê Phước Thịnh

21 tháng 2 2022

Chọn D

Đúng(1)

Trinh Quynh Nhi

21 tháng 2 2022

thanks nha

Đúng(0)

Tran Dai Quy

17 tháng 6 2021

Cho Δ: 2x-y+1=0 , (C): \(x^2+y^2-2x+4y-1=0\) , \(\overrightarrow{v}\) (3,-1)
Tìm ảnh của Δ và (C) qua \(T_{\overrightarrow{v}}\)

#Toán lớp 11

Trần Ái Linh

17 tháng 6 2021

Gọi `A(0;1)` và `B(1;3)` là 2 điểm thuộc `\Delta`

`T_(\vec v): \Delta -> \Delta'`

`<=> T_(\vec v): A(0;1) -> A'(3;0) ; B(1;3) -> B'(4;2)`

`=> \vec(A'B') (1;2)`

`=> \Delta' : 1(x-3)+2(y-0)=0 <=> x+2y-3=0`

`(C)` có: `I(1;-2)` và `R=\sqrt6 =R'`

`T_(\vec v): (C) -> (C') => T_(\vecv): I (1;-2) -> I'(4;-3)`

`=> (C'): (x-4)^2 +(y+3)^2=6`

Đúng(0)

Trần Ái Linh

17 tháng 6 2021

- Lâu không làm, không biết có đúng khum...

Đúng(0)

Pham Trong Bach

27 tháng 10 2017

Tính Δ y và ∆ y ∆ x của các hàm số sau theo x và Δ x : y = 2 x 3

#Toán lớp 11

Cao Minh Tâm

27 tháng 10 2017

Giải bài tập Toán 11 | Giải Toán lớp 11

Đúng(0)

Pham Trong Bach

29 tháng 9 2018

Tính Δ y và ∆ y ∆ x của các hàm số sau theo x và Δ x : y = 1 x

#Toán lớp 11

Cao Minh Tâm

29 tháng 9 2018

Giải bài tập Toán 11 | Giải Toán lớp 11

Đúng(0)

Pham Trong Bach

18 tháng 11 2017

Tính Δ y và ∆ y ∆ x của các hàm số sau theo x và Δ x : y = 2x - 5

#Toán lớp 11

Cao Minh Tâm

18 tháng 11 2017

Giải bài tập Toán 11 | Giải Toán lớp 11

Đúng(0)

Buddy

20 tháng 8 2023

Cho hàm số \(u = \sin x\) và hàm số \(y = {u^2}\).

a) Tính \(y\) theo \(x\).

b) Tính \(y{'_x}\) (đạo hàm của \(y\) theo biến \(x\)), \(y{'_u}\) (đạo hàm của \(y\) theo biến \(u\)) và \(u{'_x}\) (đạo hàm của \(u\) theo biến \(x\)) rồi so sánh \(y{'_x}\) với \(y{'_u}.u{'_x}\).

#Toán lớp 11

Nguyễn Lê Phước Thịnh

20 tháng 8 2023

a: \(y=u^2=\left(sinx\right)^2\)

b: \(y'\left(x\right)=\left(sin^2x\right)'=2\cdot sinx\cdot cosx\)

\(y'\left(u\right)=\left(u^2\right)'=2\cdot u\)

\(u'\left(x\right)=\left(sinx\right)'=cosx\)

=>\(y'\left(x\right)=y'\left(u\right)\cdot u'\left(x\right)\)

Đúng(1)

Buddy

17 tháng 8 2023

Cho các hàm số \(y = {u^2}\) và \(u = {x^2} + 1.\)

a) Viết công thức của hàm hợp \(y = {\left( {u\left( x \right)} \right)^2}\) theo biến x.

b) Tính và so sánh: \(y'\left( x \right)\) và \(y'\left( u \right).u'\left( x \right)\)

#Toán lớp 11

Hà Quang Minh

Giáo viên

24 tháng 8 2023

\(a,y=\left(u\left(x\right)\right)^2=\left(x^2+1\right)^2=x^4+2x^2+1\\ b,y'\left(x\right)=4x^3+4x,u'\left(x\right)=2x,y'\left(u\right)=2u\\ \Rightarrow y'\left(u\right)\cdot u'\left(x\right)=2u\cdot2x=4x\left(x^2+1\right)=4x^3+4x\)

Vậy \(y'\left(x\right)=y'\left(u\right)\cdot u'\left(x\right)\)

Đúng(0)

Nho Dora

21 tháng 4 2022

cho hàm số y=f(x)=-x³+2x²-x+5 có đồ thị (C). Tìm tham số m để tiếp tuyến Δ của đồ thị (C) tại tiếp điểm A(2;3) song song với đường thẳng (d): (m²-3m-5)x-y-2m+19=0

#Toán lớp 11

Nguyễn Việt Lâm

Giáo viên

23 tháng 4 2022

\(\left(m^2-3m-5\right)x-y-2m+19=0\)

\(\Leftrightarrow y=\left(m^2-3m-5\right)x-2m+19\)

Ta có:

\(f'\left(x\right)=-3x^2+4x-1\)

\(f'\left(2\right)=-5\)

Phương trình tiếp tuyến tại A:

\(y=-5\left(x-2\right)+3\Leftrightarrow y=-5x+13\)

Để hai đường thẳng song song:

\(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m-5=-5\\-2m+19\ne13\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m=0\\2m\ne6\end{matrix}\right.\)

\(\Leftrightarrow m=0\)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP