Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,y=\left(u\left(x\right)\right)^2=\left(x^2+1\right)^2=x^4+2x^2+1\\ b,y'\left(x\right)=4x^3+4x,u'\left(x\right)=2x,y'\left(u\right)=2u\\ \Rightarrow y'\left(u\right)\cdot u'\left(x\right)=2u\cdot2x=4x\left(x^2+1\right)=4x^3+4x\)
Vậy \(y'\left(x\right)=y'\left(u\right)\cdot u'\left(x\right)\)

a: \(y=f\left(x^2\right)=sin\left(x^2\right)\)
b: \(y=f\left(g\left(x\right)\right)=f\left(x^2\right)=sinx^2\)

y' = f'(x)
Nếu y' > 0, ∀x ∈ (a,b) hàm số đồng biến trên khoảng (a; b)
Nếu y' < 0, ∀x ∈ (a,b) hàm số f(x) nghịch biến trên khoảng (a; b)
Nếu y' = 0, ∀x ∈ (a,b) hàm số f(x) không đổi trên khoảng (a; b)
\(y'=\dfrac{-2-m}{\left(x-1\right)^2}\Rightarrow y'\left(2\right)=\dfrac{-2-m}{\left(2-1\right)^2}=-2-m\)
\(\Rightarrow-2-m=-3\Rightarrow m=1\)

Hàm \(y=\dfrac{ax+b}{cx+d}\) có đạo hàm \(y'=\dfrac{ad-bc}{\left(cd+d\right)^2}\)
Do đó: \(y'=\dfrac{5m-n}{\left(x+5\right)^2}\)

Hàm số a,b là các hàm số logarit
a: \(log_{\sqrt{3}}x\)
Cơ số là \(\sqrt{3}\)
b: \(log_{2^{-2}}x\)
Cơ số là \(2^{-2}=\dfrac{1}{4}\)

a. \(y'\left(x_0\right)=-2x_0+3\)
b. phương trình tiếp tuyến tại x0 =2 là
\(y=y'\left(x_0\right)\left(x-x_0\right)+y_0=-\left(x-2\right)+0\text{ hay }y=-x+2\)
c.\(y_0=0\Rightarrow\orbr{\begin{cases}x_0=1\\x_0=2\end{cases}\Rightarrow PTTT\orbr{\begin{cases}y=x-1\\y=-x+2\end{cases}}}\)
d. vì tiếp tuyến vuông góc với đường thẳng có hệ số góc bằng 1 nên tiếp tuyến có hệ số góc = -1
hay \(-2x_0+3=-1\Leftrightarrow x_0=2\Rightarrow PTTT:y=-x+2\)

1a.
\(y'=3x^2.f'\left(x^3\right)-2x.g'\left(x^2\right)\)
b.
\(y'=\dfrac{3f^2\left(x\right).f'\left(x\right)+3g^2\left(x\right).g'\left(x\right)}{2\sqrt{f^3\left(x\right)+g^3\left(x\right)}}\)
2.
\(f'\left(x\right)=\left(m-1\right)x^3+\left(m-2\right)x^2-2mx+3=0\)
Để ý rằng tổng hệ số của vế trái bằng 1 nên pt luôn có nghiệm \(x=1\), sử dụng lược đồ Hooc-ne ta phân tích được:
\(\Leftrightarrow\left(x-1\right)\left[\left(m-1\right)x^2+\left(2m-3\right)x-3\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(m-1\right)x^2+\left(2m-3\right)x-3=0\left(1\right)\end{matrix}\right.\)
Xét (1), với \(m=1\Rightarrow x=-3\)
- Với \(m\ne1\Rightarrow\Delta=\left(2m-3\right)^2+12\left(m-1\right)=4m^2-3\)
Nếu \(\left|m\right|< \dfrac{\sqrt{3}}{2}\Rightarrow\) (1) vô nghiệm \(\Rightarrow f'\left(x\right)=0\) có đúng 1 nghiệm
Nếu \(\left|m\right|>\dfrac{\sqrt{3}}{2}\Rightarrow\left(1\right)\) có 2 nghiệm \(\Rightarrow f'\left(x\right)=0\) có 3 nghiệm
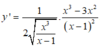
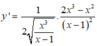
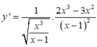
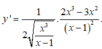
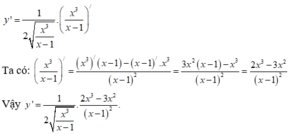
a: \(y=u^2=\left(sinx\right)^2\)
b: \(y'\left(x\right)=\left(sin^2x\right)'=2\cdot sinx\cdot cosx\)
\(y'\left(u\right)=\left(u^2\right)'=2\cdot u\)
\(u'\left(x\right)=\left(sinx\right)'=cosx\)
=>\(y'\left(x\right)=y'\left(u\right)\cdot u'\left(x\right)\)