NN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NA
Ngoc Anh Thai
Giáo viên
15 tháng 5 2021
\(A=cos^2x+\dfrac{1+cos\left(\dfrac{2\pi}{3}+2x\right)}{2}+\dfrac{1+cos\left(\dfrac{2\pi}{3}-2x\right)}{2}\\ =cos^2x+1+\dfrac{cos\left(\dfrac{2\pi}{3}+2x\right)+cos\left(\dfrac{2\pi}{3}-2x\right)}{2}\\ =cos^2x+1+cos\left(\dfrac{2\pi}{3}\right).cos2x\\ =cos^2x+1-\dfrac{1}{2}.cos2x=\dfrac{1+cos2x}{2}+1-\dfrac{cos2x}{2}=\dfrac{3}{2}.\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 2 2019
\(\dfrac{1+cos2a-sin2a}{1+cos2a+sin2a}=\dfrac{2cos^2a-2sina.cosa}{2cos^2a+2sinacosa}\)
\(=\dfrac{2cosa\left(cosa-sina\right)}{2cosa\left(cosa+sina\right)}=\dfrac{cosa-sina}{cosa+sina}=\dfrac{\sqrt{2}sin\left(\dfrac{\pi}{4}-a\right)}{\sqrt{2}cos\left(\dfrac{\pi}{4}-a\right)}=tan\left(\dfrac{\pi}{4}-a\right)\)
\(\dfrac{1+cos2a-cosa}{sin2a-sina}=\dfrac{2cos^2a-cosa}{2sina.cosa-sina}=\dfrac{cosa\left(2cosa-1\right)}{sina\left(2cosa-1\right)}=\dfrac{cosa}{sina}=cota\)
TP
2
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
28 tháng 9 2023
\(VT=\cos^2a-2.\dfrac{1}{2}\left[\cos\left(a+b\right)+\cos\left(a-b\right)\right].\cos\left(a+b\right)+\cos^2\left(a+b\right)=\)
\(=\cos^2a-\cos^2\left(a+b\right)-\cos\left(a+b\right)\cos\left(a-b\right)+\cos^2\left(a+b\right)=\)
\(=\cos^2a-\dfrac{1}{2}\left(\cos2a+\cos2b\right)=\)
\(=\dfrac{2\cos^2a-\cos^2a+\sin^2a-1+2\sin^2b}{2}=\)
\(=\dfrac{\left(\cos^2a+\sin^2a\right)-1+2\sin^2b}{2}=\sin^2b=VP\)
28 tháng 9 2023
cos2a - cos (a+b) (2 cosa . cosb - cos (a+b) = sin2b
Cos2a - ( cos a.cosb- sina .sinb)( 2 cosa .cosb - ( cosa .cosb - sina .sinb) = sin2b
cos2a - (cosa.cosb - sina.sinb) (cosa.cosb + sina .sinb) = sin2b
cos2a - ( cos2a . cos2b - sin2a .sin2b = sin2b ) .
1 - sin2a - ( 1 - sin2a ) ( 1 - sin2b) - sin2a .sin2b = sin2b
1 - sin2a - ( 1- sin2b - sin2a + sin2a .sin2b - sin2 a .sin2b = sin2b
1 - sin2a -1 + sin2 b + sin2a = sin2b
Sin2b = Sin2b điều đã CM
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2019
\(sin^6a+cos^6a=\left(sin^2x\right)^3+\left(cos^2x\right)^3\)
\(=\left(sin^2x+cos^2x\right)\left(sin^4x+cos^4x-sin^2x.cos^2x\right)\)
\(=sin^4x+2sin^2xcos^2x+cos^4x-3sin^2x.cos^2x\)
\(=\left(sin^2x+cos^2x\right)^2-\frac{3}{4}.\left(2sinx.cosx\right)^2\)
\(=1-\frac{3}{4}sin^22x=1-\frac{3}{4}\left(\frac{1}{2}-\frac{1}{2}cos4x\right)=\frac{5}{8}+\frac{3}{8}cos4x\)
2/
\(\frac{1+sin2a-cos2a}{1+cos2a}=\frac{1+2sina.cosa-\left(1-2sin^2a\right)}{1+2cos^2a-1}=\frac{2sina.cosa+2sin^2a}{2cos^2a}\)
\(=\frac{2sina.cosa}{2cos^2a}+\frac{2sin^2a}{2cos^2a}=tana+tan^2a\)
CM
28 tháng 5 2018
Chọn A.
Ta có: A= cos2( x-a) + cos2x -2cos a.cos x.cos( a - x).
= cos( x - a) [ cos(x - a) – 2cosa. cosx] + cos2x
= cos( x - a) [ cos x.cosa + sina.sinx – 2cosa.cosx] + cos2x
= cos( x - a) [ -cos x.cosa + sina.sinx] + cos2x
= -cos( x - a) .cos( x + a) + cos2x
29 tháng 7 2023
b: =1/2*[cos(10x-4x)-cos(10x+4x)]-1/2*[cos(11x-3x)-cos(11x+3x)]-1/2*[cos(7x-x)-cos(7x+x)]
=1/2*[cos 6x-cos14x-cos8x+cos14x-cos6x+cos8x]
=0
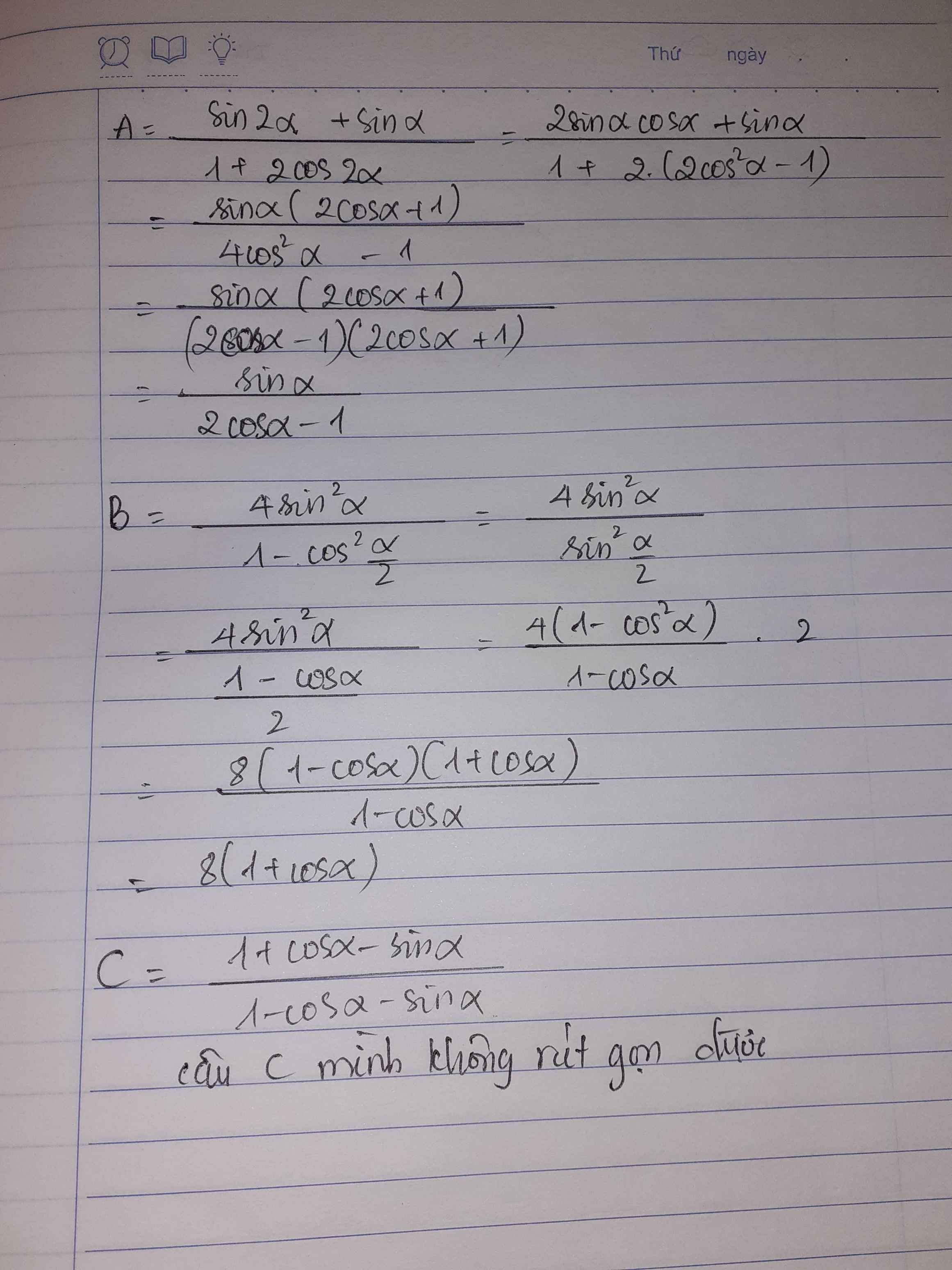
Cũng học thầy Dũng hả?