Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi ![]() với
với ![]()
Do A, B đối xứng nhau qua điểm M(3;3) nên M là trung điểm của AB.
Tính được: ![]()

Lời giải:
Gọi \(D=(a,b,c)\). Tính toán: \(\left\{\begin{matrix} \overrightarrow{AB}=(2,2,1)\\ \overrightarrow{BC}=(2,-7,1)\\ \overrightarrow{AC}=(4,-5,2)\end{matrix}\right.\)
Thấy \(\overrightarrow{AB}.\overrightarrow{AC}=0\Rightarrow\overrightarrow{AB}\perp \overrightarrow{AC}\) nên \(A,B,C,D\) là bốn đỉnh của hình chữ nhật $ABDC$
Ta có \(\overrightarrow{AC}+\overrightarrow{AB}=\overrightarrow{AD}\Leftrightarrow (4,-5,2)+(2,2,1)=(a-2,b-1,c+3)\)
\(\Leftrightarrow \left\{\begin{matrix} a-2=6\\ b-1=-3\\ c+3=3\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=8\\ b=-2\\ c=0\end{matrix}\right.\)

Gọi G là trọng tâm tam giác ABC \(\Rightarrow G\left(2;1;0\right)\)
\(T=MA^2+MB^2+MC^2\)
\(T=\left(\overrightarrow{MG}+\overrightarrow{GA}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GB}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GC}\right)^2\)
\(T=3MG^2+GA^2+GB^2+GC^2+2\overrightarrow{MG}\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)\)
\(T=3MG^2+GA^2+GB^2+GC^2\)
Do \(GA^2+GB^2+GC^2\) cố định nên \(T_{min}\) khi \(MG_{min}\)
\(\Rightarrow M\) là hình chiếu vuông góc của G lên (P)
Gọi (d) là đường thẳng qua G và vuông góc (P) \(\Rightarrow\) pt (d): \(\left\{{}\begin{matrix}x=2+t\\y=1+t\\z=t\end{matrix}\right.\)
M là giao điểm (d) và (P) nên thỏa mãn:
\(2+t+1+t+t=0\Leftrightarrow t=-1\) \(\Rightarrow M\left(1;0;-1\right)\)

\(\overrightarrow{AB}=\left(2;3;2\right)\Rightarrow AB=\sqrt{2^2+3^2+2^2}=\sqrt{17}\)
\(\overrightarrow{BC}=\left(-3;0;-1\right)\Rightarrow BC=\sqrt{\left(-3\right)^2+0^2+\left(-1\right)^2}=\sqrt{10}\)
\(\left[\overrightarrow{AB};\overrightarrow{BC}\right]=\left(-3;-4;9\right)\)
Mặt phẳng (ABC) nhận (-3;-4;9) là 1 vtpt
Phương trình (ABC):
\(-3\left(x-1\right)-4\left(y+2\right)+9\left(z-4\right)=0\)
\(\Leftrightarrow-3x-4y+9z-41=0\)
\(d\left(M;\left(ABC\right)\right)=\dfrac{\left|-3.2+4.1+9.3-41\right|}{\sqrt{\left(-3\right)^2+\left(-4\right)^2+9^2}}=\dfrac{8\sqrt{106}}{53}\)

Câu 1:
\(y=x^3-3x^2-2\Rightarrow y'=3x^2-6x\)
Gọi hoành độ của M là \(x_M\)
Hệ số góc của tiếp tuyến của đồ thị (C) tại M bằng 9 tương đương với:
\(f'(x_M)=3x_M^2-6x_M=9\)
\(\Leftrightarrow x_M=3\) hoặc $x_M=-1$
\(\Rightarrow y_M=-2\) hoặc \(y_M=-6\)
Vậy tiếp điểm có tọa độ (3;-2) hoặc (-1;-6)
Đáp án B
Câu 2:
Gọi hoành độ tiếp điểm là $x_0$
Hệ số góc của tiếp tuyến tại tiếp điểm là:
\(f'(x_0)=x_0^2-4x_0+3\)
Vì tt song song với \(y=3x-\frac{20}{3}\Rightarrow f'(x_0)=3\)
\(\Leftrightarrow x_0^2-4x_0+3=3\Leftrightarrow x_0=0; 4\)
Khi đó: PTTT là:
\(\left[{}\begin{matrix}y=3\left(x-0\right)+f\left(0\right)=3x+4\\y=3\left(x-4\right)+f\left(4\right)=3x-\dfrac{20}{3}\end{matrix}\right.\) (đt 2 loại vì trùng )
Do đó \(y=3x+4\Rightarrow \) đáp án A
Câu 3:
PT hoành độ giao điểm:
\(\frac{2x+1}{x-1}-(-x+m)=0\)
\(\Leftrightarrow x^2+(1-m)x+(m+1)=0\) (1)
Để 2 ĐTHS cắt nhau tại hai điểm pb thì (1) phải có hai nghiệm phân biệt
\(\Leftrightarrow \Delta=(1-m)^2-4(m+1)> 0\)
\(\Leftrightarrow m^2-6m-3> 0\)
\(\Leftrightarrow\left[{}\begin{matrix}m< 3-2\sqrt{3}\\m>3+2\sqrt{3}\end{matrix}\right.\)
Kết hợp với m nguyên và \(m\in (0;10)\Rightarrow m=7;8;9\)
Có 3 giá trị m thỏa mãn.
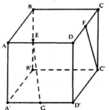


Đáp án D
Hướng dẫn giải: Ta có
Gọi (P) là mặt phẳng chứa C'F và song song với EG, do đó:
Lại có (P):