Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.DE=\dfrac{10+6}{2}.5=40\left(cm^2\right)\)
b) Xem hình vẽ
Tam giác vuông EAD có: \(AE=\sqrt{AD^2-DE^2}=\sqrt{5^2-4^2}=3\)
Vì ABCD là hình thang cân nên AE = FB = 3.
Suy ra AB = EF + AE + FB = 6 + 3 + 3 = 12.
\(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.DE=\dfrac{12+6}{2}.4=36\left(cm^2\right)\)

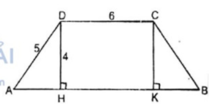
Xét hình thang cân ABCD có AB // CD
Đáy nhỏ CD = 6cm, cạnh bên AD = 5cm
Đường cao DH = 4cm. Kẻ CK ⊥ AB
Ta có tứ giác CDHK là hình chữ nhật
HK = CD = 6cm
△ AHD vuông tại H. Theo định lý Pi-ta-go ta có: A D 2 = A H 2 + D H 2
⇒ A H 2 = A D 2 - D H 2 = 5 2 - 4 2 = 25 – 16 = 9 ⇒ AH = 3cm
Xét hai tam giác vuông DHA và CKB :
∠ (DHA)= ∠ (CKB)= 90 0
AD = BC (tính chất hình thang cân)
∠ A = ∠ B(gt)
Do đó: △ DHA = △ CKB (cạnh huyền, góc nhọn)
⇒ KB = AH = 3 (cm)
AB = AH + HK + KB = 3 + 6 + 3 = 12 (cm)
S A B C D = (AB + CD) / 2. DH = (12 + 6) / 2. 4 = 36( c m 2 )

Kẻ 2 đường cao AH và BH'
Xét hai tam giác vuông AHD và BH'C ,có :
AD = BC ( gt )
\(\widehat{D}\)=\(\widehat{C}\) ( gt )
=> tam giác AHD = tam giác BH'C ( ch - gn )
=> HD = H'C ( hai cạnh tương ứng )
Kẻ AH'
Xét tam giác ABH' và tam giác H'HA , có :
AH' : chung
góc B = góc C ( = 90o ) - AB//DC
H'B = AH ( tam giác AHD = tam giác BH'C )
=> tam giác ABH' = tam giác H'HA ( ch - cgv )
=> AB = H'H ( hai cạnh tương ứng ) => HH' = 6cm
Ta lại có : DH + HH' + H'C = 14cm
=> DH + HH' = 8cm => DH = 4cm
Xét tam giác AHD vuông tại H
=> AD2 = AH2 + HD2 ( định lý Py - ta - go )
=> 52 = AH2 + 42
=> 25 = AH2 + 16
=> AH2 = 9
=> AH = 3 hoặc AH = -3 mà AH > 0 => AH = 3cm
Vậy ...( đpcm )


Bài 2:
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{ACB}=\widehat{ACD}\)
hay CA là tia phân giác của \(\widehat{BCD}\)

kẻ 1 đg vuông góc từ B cắt DC tại K
xét tg ADH và tg BCK :
góc AHD= góc BKC ( = 90 độ )
AD= BC ( gt )
góc ADH= góc BCK ( gt )
=> tg ADH= tg BCK ( ch- gn)
=> DH= KC ( 2 cạnh t/ứ ) ( 1)
vì AB song song DC=> ABKD là hcn ( tự chứng minh)
=> AB=Dk= 8 cm
=> DH= KC= (DC-DK ) :2= 3 cm
áp dụng đlí pi-ta-go cho tg ADH vuông ở H :
AH2+DH2= AD2
TS : AH2= 52-32
=> AH = 4 cm

Kẻ AH ⊥ CD, BK ⊥ CD thì AH//BK nên hình thang ABKH có hai cạnh bên song song.
Áp dụng tính chất của hình thang ABKH có hai cạnh bên song song, ta có: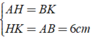
Áp dụng định lí Py – ta – go vào tam giác ADH vuông tại H ta được:
Vậy chiều cao của hình thang cân là 3cm.