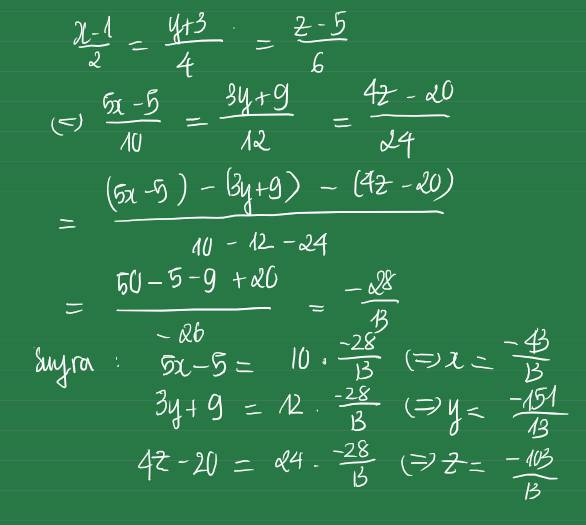K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 7 2021
Đề là \(\dfrac{2}{3}x=\dfrac{3}{4}y=\dfrac{4}{5}z\) và \(x+y-z=57\)
hay \(\dfrac{2}{3x}=\dfrac{3}{4x}=\dfrac{4}{5z}\) \(x+y-z=57\)
30 tháng 7 2021
Ta có: \(\dfrac{2}{3}x=\dfrac{3}{4}y=\dfrac{4}{5}z\)
nên \(\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}\)
mà x+y-z=57
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}=\dfrac{x+y-z}{\dfrac{3}{2}+\dfrac{4}{3}-\dfrac{5}{4}}=\dfrac{57}{\dfrac{19}{12}}=36\)
Do đó:
\(\left\{{}\begin{matrix}x=36\cdot\dfrac{3}{2}=54\\y=36\cdot\dfrac{4}{3}=48\\z=36\cdot\dfrac{5}{4}=45\end{matrix}\right.\)
BT
1
14 tháng 9 2019
\(\frac{x}{4}=\frac{y}{3};3y=5z\) và x + y + z = 75
Ta có: \(\hept{\begin{cases}\frac{x}{4}=\frac{y}{3}\\3y=5z\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x}{4}=\frac{y}{3}\\\frac{y}{5}=\frac{z}{3}\end{cases}}\)
=> \(\frac{x}{4}=\frac{y}{3};\frac{y}{5}=\frac{z}{3}\)
=> \(\frac{x}{20}=\frac{y}{15};\frac{y}{15}=\frac{z}{9}\)
=> \(\frac{x}{20}=\frac{y}{15}=\frac{z}{9}\)
Áp dụng t/c dãy tỉ số bằng nhau ta có :
\(\frac{x}{20}=\frac{y}{15}=\frac{z}{9}=\frac{x+y+z}{20+15+9}=\frac{75}{44}\)
=> \(\hept{\begin{cases}\frac{x}{20}=\frac{75}{44}\\\frac{y}{15}=\frac{75}{44}\\\frac{z}{9}=\frac{75}{44}\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{375}{11}\\y=\frac{1125}{44}\\z=\frac{675}{44}\end{cases}}\)
\(3x=4y;2y=5z\)và x + y - z = 58
Ta có : \(\hept{\begin{cases}3x=4y\\2y=5z\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x}{4}=\frac{y}{3}\\\frac{y}{5}=\frac{z}{2}\end{cases}}\)
=> \(\frac{x}{4}=\frac{y}{3};\frac{y}{5}=\frac{z}{2}\)
Từ \(\hept{\begin{cases}\frac{x}{4}=\frac{y}{3}\Rightarrow\frac{x}{20}=\frac{y}{15}\\\frac{y}{5}=\frac{z}{2}\Rightarrow\frac{y}{15}=\frac{z}{6}\end{cases}\Rightarrow\frac{x}{20}=\frac{y}{15}=\frac{z}{6}=\frac{x+y-z}{20+15-6}=\frac{58}{29}=2}\)
=> \(\hept{\begin{cases}\frac{x}{20}=2\\\frac{y}{15}=2\\\frac{z}{6}=2\end{cases}}\Rightarrow\hept{\begin{cases}x=40\\y=30\\z=12\end{cases}}\)
D
2
13 tháng 3 2021
Ta có: x-1/2 = y+3/4 = z-5/6 = K
x = 2K+1 ; y = 4K+3 ; z = 6K+5
Thay các giá trị: x = 2K+1 ; y = 4K-3 ; z = 6K+5 vào biểu thức
5z - 3x - 4y = 50. Ta có,
5.(6K+5) - 3.(4K+3) - 4.(4K-3) = 50
<=> 30K + 25 - 6K - 3 - 16K + 12 = 50
<=> 8K + 34 = 50
<=> 8K = 50-34 = 16
<=> K = 16/8 = 2
=> x-1/2 = 2 => x-1 = 2.2 <=> x-1=4 => x=4+1=5
=>y-3/4 = 2 => y+3 = 2.4 <=> y+3 = 8 => y = 8-3=5
=> z-5/6 = 2 => z-5 = 2.6 <=> z-5 = 12 => z = 12+5=17
B
1
21 tháng 10 2021
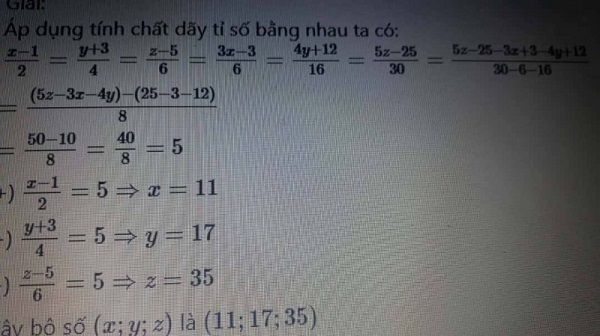
Áp dụng t/c dtsbn:
\(\dfrac{x-1}{2}=\dfrac{y+3}{4}=\dfrac{z-5}{6}=\dfrac{3x-3}{6}=\dfrac{4y+12}{16}=\dfrac{5z-25}{30}=\dfrac{-3x+3-4y-12+5z-25}{-6-16+30}=\dfrac{50+3-12-25}{8}=\dfrac{16}{8}=2\\ \Rightarrow\left\{{}\begin{matrix}x-1=4\\y+3=8\\z-5=12\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=5\\y=5\\z=17\end{matrix}\right.\)
TD
1
H
1
AH
Akai Haruma
Giáo viên
28 tháng 10 2023
Lời giải:
Đặt $\frac{x-1}{2}=\frac{y+3}{4}=\frac{z-5}{6}=a$
$\Rightarrow x=2a+1; y=4a-3; z=6a+5$
Thay vào điều kiện $5z-3x-4y=50$ thì:
$5(6a+5)-3(2a+1)-4(4a-3)=50$
$\Rightarrow 8a-16=0$
$\Rightarrow a=2$
Do đó:
$x=2a+1=2.2+1=5$
$y=4a-3=4.2-3=5$
$z=6a+5=6.2+5=17$