
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


( x - 1 )2018 + (y - 2 )2020+(z-3)2022=0
\(\Leftrightarrow\left\{{}\begin{matrix}x-1=0\\y-2=0\\z-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\\z=3\end{matrix}\right.\)
\(A=\dfrac{1}{9}\left(-x\right)^{2021}y^2z^3=\dfrac{1}{3}\left(-1\right)^{2021}.2^2.3^3=\dfrac{1}{3}.\left(-1\right).4.27=-36\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{-4}{x}=\dfrac{6}{y}=\dfrac{\left(-4\right)\cdot\left(-5\right)+6\cdot6}{-5x+6y}=\dfrac{56}{448}=\dfrac{1}{8}\)
Do đó: x=-32; y=48

\(a,2\left|3x-1\right|+1=5\\ \Rightarrow2\left|3x-1\right|=5-1\\ \Rightarrow2\left|3x-1\right|=4\\ \Rightarrow\left|3x-1\right|=4:2\\ \Rightarrow\left|3x-1\right|=2\\ \Rightarrow\left[{}\begin{matrix}3x-1=2\\3x-1=-2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}3x=3\\3x=-1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\)
\(b,\left|\dfrac{x}{2}-1\right|=3\\ \Rightarrow\left[{}\begin{matrix}\dfrac{x}{2}-1=3\\\dfrac{x}{2}-1=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}\dfrac{x}{2}=4\\\dfrac{x}{2}=-2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=8\\x=-4\end{matrix}\right.\)
\(c,\left|-x+\dfrac{2}{5}\right|+\dfrac{1}{2}=3,5\\ \Rightarrow\left|-x+\dfrac{2}{5}\right|=3,5-\dfrac{1}{2}\\ \Rightarrow\left|-x+\dfrac{2}{5}\right|=3\\ \Rightarrow\left[{}\begin{matrix}-x+\dfrac{2}{5}=3\\-x+\dfrac{2}{5}=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}-x=\dfrac{13}{5}\\-x=-\dfrac{17}{5}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{13}{5}\\x=\dfrac{17}{5}\end{matrix}\right.\)
\(d,\left|x-\dfrac{1}{3}\right|=2\dfrac{3}{5}\\ \Rightarrow\left|x-\dfrac{1}{3}\right|=\dfrac{13}{5}\\ \Rightarrow\left[{}\begin{matrix}x-\dfrac{1}{3}=\dfrac{13}{5}\\x-\dfrac{1}{3}=-\dfrac{13}{5}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{13}{5}+\dfrac{1}{3}\\x=-\dfrac{13}{5}+\dfrac{1}{3}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}\dfrac{44}{15}\\x=-\dfrac{34}{15}\end{matrix}\right.\)

Xin lỗi chị nhiề vì em mới lớp 5 chị nhé nếu đươc em sẽ giúp chị ak


\(x^2+2y^2-2xy+4y+3< 0\)
\(\Rightarrow x^2-2xy+y^2+y^2+4y+4-1< 0\)
\(\Rightarrow\left(x^2-2xy+y^2\right)+\left(y^2+4y+4\right)-1< 0\)
\(\Rightarrow\left(x-y\right)^2+\left(y+2\right)^2-1< 0\)
Mà: \(\left\{{}\begin{matrix}\left(x-y\right)^2\ge0\forall x,y\\\left(y+2\right)^2\ge0\forall y\end{matrix}\right.\)
\(\Rightarrow\left(x-y\right)^2+\left(y+2\right)^2-1\ge-1\forall x,y\)
Mặt khác: \(\left(x-y\right)^2+\left(y+2\right)^2-1< 0\)
Dấu "=" xảy ra:
\(\left\{{}\begin{matrix}x-y=0\\y+2=0\end{matrix}\right.\)
\(\Rightarrow x=y=-2\)
Vậy: ....

 giúp với mình đang vội:(((
giúp với mình đang vội:(((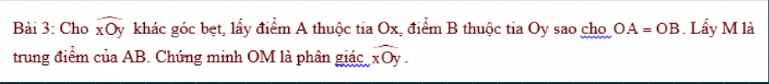
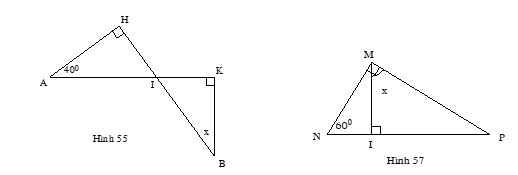
Hình 55:
Xét tam giác AHI và tam giác BKI lần lượt vg tại H,K có:
\(\left\{{}\begin{matrix}\widehat{HAI}+\widehat{HIA}=90^0\\x+\widehat{KIB}=90^0\end{matrix}\right.\)
Mà \(\widehat{HIA}=\widehat{KIB}\)(đối đỉnh)
\(\Rightarrow x=\widehat{HAI}=40^0\)
Hình 57:
Xét tam giác MNP vg tại M và tam giác MIP vg tại I:
\(\left\{{}\begin{matrix}\widehat{N}+\widehat{NMI}=90^0\\x+\widehat{NMI}=90^0\end{matrix}\right.\)
\(\Rightarrow x=\widehat{N}=60^0\)
x1=40 độ
x2=60 độ
Có cần giải thích chi tiết ko bạn