TN
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
0
DD
0
DN
1
14 tháng 6 2023
c: =>x+y-xy=-16
=>x+y-xy-1=-17
=>x(1-y)-(1-y)=-17
=>(1-y)(x-1)=-17
=>(x-1;y-1)=17
=>(x-1;y-1) thuộc {(1;17); (17;1); (-1;-17); (-17;-1)}
=>(x,y) thuộc {(2;18); (18;2); (0;-16); (-16;0)}
b: Tham khảo:
CS
2
PT
22 tháng 4 2021
Bài 1: Ta có 200920 = (20092)10 = (2009.2009)10
2009200910 = (10001.2009)10
Mà 2009 < 10001 ➩ (2009.2009)10 < (10001.2009)10
Vậy 200920 < 2009200910
1 tháng 8 2023
10:
Vì n là số lẻ nên n=2k-1
Số số hạng là (2k-1-1):2+1=k(số)
Tổng là (2k-1+1)*k/2=2k*k/2=k^2 là số chính phương
11:
n^3-n^2+2n+7 chia hết cho n^2+1
=>n^3+n-n^2-1+n+8 chia hết cho n^2+1
=>n+8 chia hết cho n^2+1
=>n^2-64 chia hết cho n^2+1
=>n^2+1-65 chia hết cho n^2+1
=>n^2+1 thuộc {1;5;13;65}
=>\(n\in\left\{0;2;-2;2\sqrt{3};-2\sqrt{3};8;-8\right\}\)
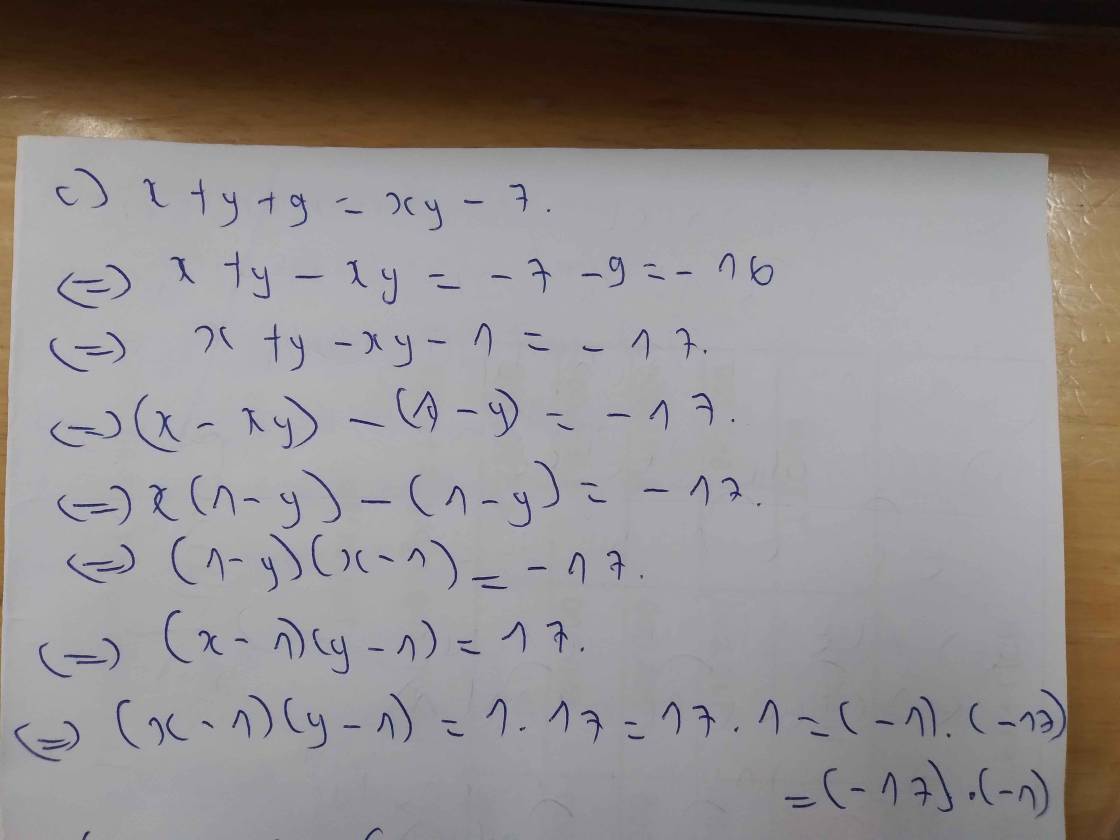
c) \(x+y+9=xy-7\)
=> \(x+y+16=xy=>x+16=xy-y=y.\left(x-1\right)\)
\(=>y=\frac{x+16}{x-1}\) (x khác 1)
Mà do y thuộc Z => \(\frac{x+16}{x-1}\in Z=>x+16⋮x-1=>\left(x-1\right)+17⋮x-1=>x-1\inƯ\left(17\right)=\left\{\pm1;\pm17\right\}\)
\(=>x\in\left\{0;2;-16;18\right\}\) (Thỏa mãn do khác 1)
*) Nếu x=0 => 16+y=0=> y=-16.
*) Nếu x=2 => 18+y=2y=> y=18
*) Nếu x=-16 => y=-16y => y=0
*) Nếu x=18 => y=2
Vậy (x,y)=.....
sao ko có lời giải 2 câu trên ak tui cần 2 câu trên