K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
15 tháng 2 2018
Đáp án C
G T ⇔ x 2 + y − 3 x + y 2 − 4 y + 4 = 0 y 2 + x − 4 y + x 2 − 3 x + 4 = 0
có nghiệm ⇔ Δ x ≥ 0 Δ y ≥ 0 ⇔ 0 ≤ x ≤ 4 3 1 ≤ y ≤ 7 3
Và:
x y = 3 x + 4 y − x 2 − y 2 − 4 ⇒ P = 3 x 3 + 18 x 2 + 45 x − 8 ⏟ f x + − 3 y 3 + 3 y 2 + 8 y ⏟ g y
Xét hàm số f x = 3 x 3 + 18 x 2 + 45 x − 8 trên 0 ; 4 3 ⇒ max 0 ; 4 3 f x = f 4 3 = 820 9
Xét hàm số g x = − 3 y 3 + 3 y 2 + 8 y trên 1 ; 7 3 ⇒ max 1 ; 7 3 g x = f 4 3 = 80 9
Vật P ≤ max 0 ; 4 3 f x + max 1 ; 7 3 g x = 100
Dấu “=” xảy ra khi x = y = 4 3
16 tháng 4 2016
3x-2y=27-xy
3x-2y+xy=27
3x+xy-2y=27
x(3+y)-2y-6=27-6
x(3+y)-(2y+6)=21
x(3+y)-2(y+3)=21
(y+3)(x-2)=21
Ta có bảng giá trị:
| y+3 | 1 | 21 | 7 | 3 | -1 | -21 | -3 | -7 |
| y | -2 | 18 | 4 | 0 | -4 | -24 | -6 | -10 |
| x-2 | 21 | 1 | 3 | 7 | -21 | -1 | -7 | -5 |
| x | 23 | 3 | 5 | 9 | -19 | 1 | -5 | -3 |
CM
21 tháng 5 2019
Đáp án C
Từ 3 x = 4 x = 12 − x x = log 3 a y = log 4 a z = − log 12 a ⇒ P = log 3 a log 4 a − log 4 a log 12 a − log 12 a log 3 a
1
log
a
3
log
a
4
−
1
log
a
4
log
a
12
−
1
log
a
12
log
a
3
=
log
a
12
−
log
a
3
−
log
a
4
log
a
3
log
a
4
log
a
12
=
log
a
1
log
a
3
log
a
4
log
a
12
=
0
CM
6 tháng 2 2019
Đáp án C
Phương pháp:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Cách giải:
<=> 
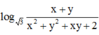
(2)
Đặt 
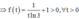
=> f(t) đồng biến trên (0;+∞)
<=> 
<=> 
Khi đó,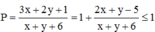 
vì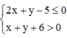 
Vậy Pmax = 1 khi và chỉ khi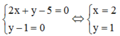 
CM
13 tháng 9 2019
Đáp án C
Phương pháp giải:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Lời giải:
log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) + x y (1)
(2)
Đặt 
=> f(t) đồng biến trên (0;+∞)
Khi đó, 
vì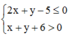 
Vậy Pmax = 1 khi và chỉ khi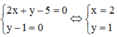 
27 tháng 4 2016
=> x(y+1)+y=5
=> x(y+1)+(y+1)=6
=> (y+1).(x+1)=6
Sau đó lập bảng nhé! OK
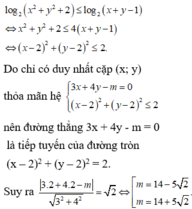
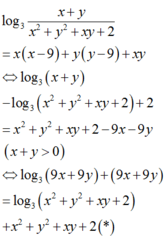
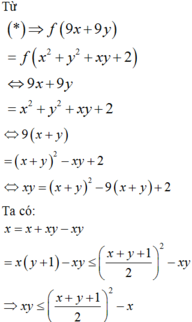
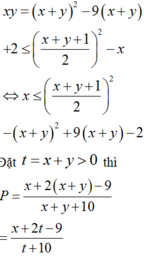
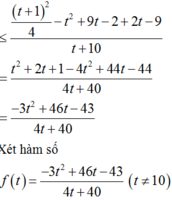
Ta có :
3x + 4y - xy = 15
=> (4 - x)(y - 3) = 3 = 1 . 3 = 3 . 1 = (-1) . (-3) = (-3) . (-1)
Xét các trường hợp trên là ra
Nếu x,y thuộc Z
suy ra phương trình tương đương với y(4-x)-3(4-x)=15-12
suy ra (4-x)(y-3)=3
Xét các trường hợp
4-x=1 thì y-3=3
4-x=-1 thì y-3= -3
4-x =3 thì y-3=1
4-x= -3 thì y-3= -1
giải các trường hợp ra tìm x và y