
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(x^4-13x^2+36=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)\left(x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\\x=-2\\x=-3\end{matrix}\right.\)
b) \(5x^4+3x^2-8=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(5x^2+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)( do \(5x^2+8\ge8>0\))
c: Ta có: \(2x^4+3x^2+2=0\)
Đặt \(a=x^2\)
Phương trình tương đương là: \(2a^2+3a+2=0\)
\(\text{Δ}=3^2-4\cdot2\cdot2=9-16=-7\)
Vì Δ<0 nên phương trình vô nghiệm
Vậy: Phương trình \(2x^4+3x^2+2=0\) vô nghiệm

a) ĐK: x ≥ 2
\(\sqrt{3x-6}=3\)
\(\Leftrightarrow3x-6=9\)
<=> 3x = 15
<=> x = 5
Vậy:....
b) ĐK: 5x - 16 ≥ 0
<=> 5x ≥ 16
<=> x ≥ 16/5
\(\sqrt{5x-16}=2\)
<=> 5x - 16 = 4
<=> 5x = 20
<=> x = 4
c) ĐK: \(x^2-4x+3\ne0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)\ne0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne1\\x\ne3\end{matrix}\right.\)
bình phương hai vế ta được:
a)điều kiện của x:x≥2
3x-6=9 <=> x=5(nhận)
b)ĐK: x≥16/5
5x-16=4 <=>x=4(nhận)
c) ta có: \(\dfrac{2x-3}{\left(x-2\right)^2-1}\)= \(\dfrac{2x-3}{\left(x-3\right)\left(x-1\right)}\)
ĐKXĐ: x≠3 ;x≠1

a) x 4 – 5 x 2 + 4 = 0 ( 1 )
Đặt x 2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : t 2 – 5 t + 4 = 0 ( 2 )
Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm t 1 = 1 ; t 2 = c / a = 4
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x 2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x 2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.
b) 2 x 4 – 3 x 2 – 2 = 0 ; ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 2 t 2 – 3 t – 2 = 0 ( 2 )
Giải (2) : Có a = 2 ; b = -3 ; c = -2
⇒ Δ = ( - 3 ) 2 - 4 . 2 . ( - 2 ) = 25 > 0
⇒ Phương trình có hai nghiệm
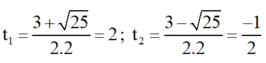
Chỉ có giá trị t 1 = 2 thỏa mãn điều kiện.
+ Với t = 2 ⇒ x 2 = 2 ⇒ x = √2 hoặc x = -√2;
Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.
c) 3 x 4 + 10 x 2 + 3 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 3 t 2 + 10 t + 3 = 0 ( 2 )
Giải (2) : Có a = 3; b' = 5; c = 3
⇒ Δ ’ = 5 2 – 3 . 3 = 16 > 0
⇒ Phương trình có hai nghiệm phân biệt
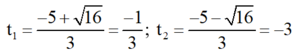
Cả hai giá trị đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.

câu trả lời của thu hương rất hay!
Mình làm được khổ nỗi lại chưa biết nghiệm là gì? @ thu hương có thể giải thích cho minh không
hiihhi

a) 4 x 4 + x 2 − 5 = 0
Đặt x 2 = t (t ≥ 0). Phương trình trở thành:
4 t 2 + t − 5 = 0
Nhận thấy phương trình có dạng a + b + c = 0 nên phương trình có nghiệm
t 1 = 1 ; t 2 = ( − 5 ) / 4
Do t ≥ 0 nên t = 1 thỏa mãn điều kiện
Với t = 1, ta có: x 2 = 1 ⇔ x = ± 1
Vậy phương trình có 2 nghiệm x 1 = 1 ; x 2 = − 1
b) 3 x 4 + 4 x 2 + 1 = 0
Đặt x 2 = t ( t ≥ 0 ) . Phương trình trở thành:
3 t 2 + 4 t + 1 = 0
Nhận thấy phương trình có dạng a - b + c = 0 nên phương trình có nghiệm
t 1 = - 1 ; t 2 = ( - 1 ) / 3
Cả 2 nghiệm của phương trình đều không thỏa mãn điều kiện t ≥ 0
Vậy phương trình đã cho vô nghiệm.

a. 2x\(^2\)-8=0
2x\(^2\)=8
x\(^2\)=4
x=2
b.3x\(^3\)-5x=0
x(3x\(^2\)-5)=0
\(\left[{}\begin{matrix}x=0\\x^2-5=0\end{matrix}\right.\)⇔\(\left[{}\begin{matrix}x=0\\x^2=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=^+_-\sqrt{5}\end{matrix}\right.\)
c.x\(^4\)+3x\(^2\)-4=0\(^{\left(\cdot\right)}\)
đặt t=x\(^2\) (t>0)
ta có pt: t\(^2\)+3t-4=0 \(^{\left(1\right)}\)
thấy có a+b+c=1+3+(-4)=0 nên pt\(^{\left(1\right)}\) có 2 nghiệm
t\(_1\)=1; t\(_2\)=\(\dfrac{c}{a}\)=-4
khi t\(_1\)=1 thì x\(^2\)=1 ⇒x=\(^+_-\)1
khi t\(_2\)=-4 thì x\(^2\)=-4 ⇒ x=\(^+_-\)2
vậy pt đã cho có 4 nghiệm x=\(^+_-\)1; x=\(^+_-\)2
d)3x\(^2\)+6x-9=0
thấy có a+b+c= 3+6+(-9)=0 nên pt có 2 nghiệm
x\(_1\)=1; x\(_2\)=\(\dfrac{c}{a}=\dfrac{-9}{3}=-3\)
e. \(\dfrac{x+2}{x-5}+3=\dfrac{6}{2-x}\) (ĐK: x#5; x#2 )
⇔\(\dfrac{\left(x+2\right)\left(2-x\right)}{\left(x-5\right)\left(2-x\right)}+\dfrac{3\left(x+2\right)\left(2-x\right)}{\left(x-5\right)\left(2-x\right)}\)=\(\dfrac{6\left(x-5\right)}{\left(x-5\right)\left(2-x\right)}\)
⇒2x - x\(^2\) + 4 - 2x + 6x - 6x\(^2\) + 12 - 6x - 6x +30 = 0
⇔-7x\(^2\) - 6x + 46=0
Δ'=b'\(^2\)-ac = (-3)\(^2\) - (-7)\(\times\)46= 9+53 = 62>0
\(\sqrt{\Delta'}=\sqrt{62}\)
vậy pt có 2 nghiệm phân biệt
x\(_1\)=\(\dfrac{-b'+\sqrt{\Delta'}}{a}=\dfrac{3+\sqrt{62}}{-7}\)
x\(_2\)=\(\dfrac{-b'-\sqrt{\Delta'}}{a}=\dfrac{3-\sqrt{62}}{-7}\)
vậy pt đã cho có 2 nghiệm x\(_1\)=.....;x\(_2\)=......
câu g làm tương tự câu c

5x3 – x2 – 5x + 1 = 0
⇔ x2(5x – 1) – (5x – 1) = 0
⇔ (x2 – 1)(5x – 1) = 0
⇔ (x – 1)(x + 1)(5x – 1) = 0
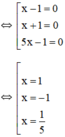
Vậy phương trình có tập nghiệm 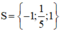

a) 1,2x3 – x2 – 0,2x = 0
⇔ 0,2x.(6x2 – 5x – 1) = 0
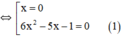
Giải (1): 6x2 – 5x – 1 = 0
có a = 6; b = -5; c = -1
⇒ a + b + c = 0
⇒ (1) có hai nghiệm x1 = 1 và x2 = c/a = -1/6.
Vậy phương trình ban đầu có tập nghiệm 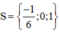
b) 5x3 – x2 – 5x + 1 = 0
⇔ x2(5x – 1) – (5x – 1) = 0
⇔ (x2 – 1)(5x – 1) = 0
⇔ (x – 1)(x + 1)(5x – 1) = 0
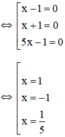
Vậy phương trình có tập nghiệm 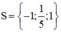

a) 3x4 - 13x3 + 16x2 - 13x + 3 = 0
(x - 3)(3x - 1)(x2 - x + 1) = 0
nhưng vì x2 - x + 1 # 0 nên:
x - 3 = 0 hoặc 3x - 1 = 0
x = 0 + 3 3x = 0 + 1
x = 3 3x = 1
x = 1/3
b) 6x4 + 5x3 - 38x2 + 5x + 6 = 0
(x - 2)(x + 3)(3x + 1)(2x - 1) = 0
x - 2 = 0 hoặc x + 3 = 0 hoặc 3x + 1 = 0 hoặc 2x - 1 = 0
x = 0 + 2 x = 0 - 3 3x = 0 - 1 2x = 0 + 1
x = 2 x = -3 3x = -1 2x = 1
x = -1/3 x = 1/2