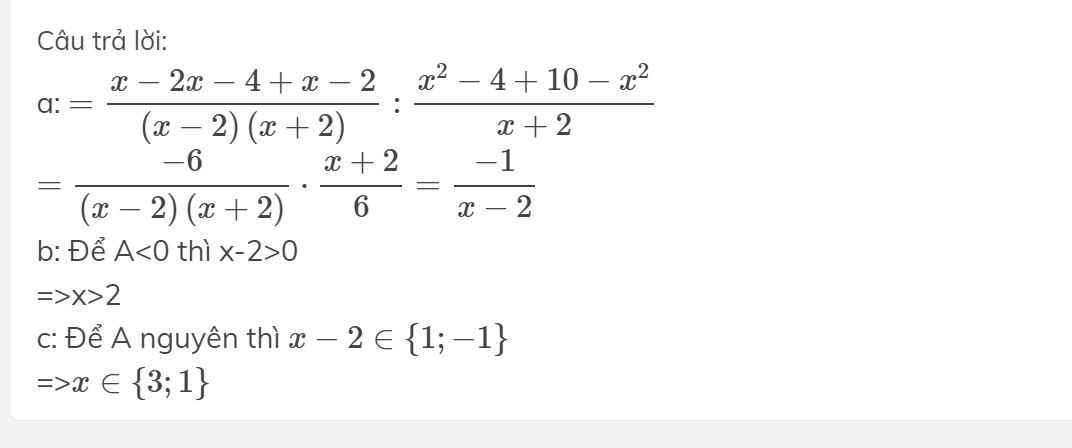VH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 10 2018
\(P=\frac{2\left(x-2\right)\left(x+2\right)}{x^2+x+5}.\frac{5\left(x^2+x+5\right)}{\left(x-4\right)\left(x+3\right)}.\frac{\left(x-1\right)\left(x-4\right)}{10\left(x-2\right)\left(x+2\right)}=\frac{x-1}{x+3}\)
ĐK: \(x\ne\left\{4;-3;1;2;-2\right\}\)
b, \(P\in Z\Rightarrow\frac{x-1}{x+3}\in Z\Rightarrow x-1⋮\left(x+3\right)\Rightarrow-4⋮\left(x+3\right)\Rightarrow\left(x+3\right)\in\left\{-4;-2;-1;1;2;4\right\}\)
\(\Rightarrow x\in\left\{-7;-5;-4;-2;-1;1\right\}\)
\(\Rightarrow P\in\left\{2;3;5;-3;-1;0\right\}\)
Y
19 tháng 1 2023
\(a,A=\dfrac{x\left(x+2\right)+\left(2-x\right)\left(x-2\right)+12-10x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+2x+2x-4-x^2+2x+12-10x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{-4x+8}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{-4\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=-\dfrac{4}{x+2}\)
Vậy \(A=-\dfrac{4}{\left(x+2\right)}\)
5 tháng 1 2022
a: Thay x=5 vào B, ta được:
\(B=\dfrac{5-1}{5-3}=\dfrac{4}{2}=2\)
b: \(A=\dfrac{2x^2+6x-2x^2-3x-1}{\left(x-3\right)\left(x+3\right)}=\dfrac{3x-1}{\left(x+3\right)\left(x-3\right)}\)
19 tháng 11 2023
a: \(A=\left(\dfrac{2x^2+2}{x^3-1}+\dfrac{x^2-x+1}{x^4+x^2+1}-\dfrac{x^2+3}{x^3-x^2+3x-3}\right):\dfrac{1}{x-1}\)
\(=\left(\dfrac{2x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{x^2-x+1}{x^4+2x^2+1-x^2}-\dfrac{x^2+3}{x^2\left(x-1\right)+3\left(x-1\right)}\right)\cdot\dfrac{x-1}{1}\)
\(=\left(\dfrac{2x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{\left(x^2-x+1\right)}{\left(x^2+1\right)^2-x^2}-\dfrac{x^2+3}{\left(x-1\right)\left(x^2+3\right)}\right)\cdot\dfrac{x-1}{1}\)
\(=\left(\dfrac{2x^2+3}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{x^2-x+1}{\left(x^2+1+x\right)\left(x^2+1-x\right)}-\dfrac{1}{x-1}\right)\cdot\dfrac{x-1}{1}\)
\(=\left(\dfrac{2x^2+3}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{1}{x^2+x+1}-\dfrac{1}{x-1}\right)\cdot\dfrac{x-1}{1}\)
\(=\dfrac{2x^2+3+x-1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\dfrac{x-1}{1}\)
\(=\dfrac{x^2+1}{x^2+x+1}\)
b: Để A là số nguyên thì \(x^2+1⋮x^2+x+1\)
=>\(x^2+x+1-x⋮x^2+x+1\)
=>\(x⋮x^2+x+1\)
=>\(x^2+x⋮x^2+x+1\)
=>\(x^2+x+1-1⋮x^2+x+1\)
=>\(-1⋮x^2+x+1\)
=>\(x^2+x+1\in\left\{1;-1\right\}\)
=>\(x^2+x+1=1\)
=>x2+x=0
=>x(x+1)=0
=>\(x\in\left\{0;-1\right\}\)
DT
0
DX
26 tháng 2 2023
\(A=\left(\dfrac{x}{x^2-4}+\dfrac{2}{2-x}+\dfrac{1}{x+2}\right):\left(x-2+\dfrac{10-x^2}{x+2}\right)\)
\(\Rightarrow A=\left(\dfrac{x-2\left(x+2\right)+1\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\right):\left(\dfrac{\left(x-2\right)\left(x+2\right)+10-x^2}{x+2}\right)\)
\(\Rightarrow A=\left(\dfrac{-6}{x^2-4}\right):\left(\dfrac{6}{x+2}\right)\)
\(\Rightarrow A=-\dfrac{6}{x^2-4}.\dfrac{x+2}{6}=-\dfrac{6\left(x+2\right)}{\left(x-2\right)\left(x+2\right)6}=-\dfrac{1}{x-2}\)
để A<0 thì :
\(\left\{{}\begin{matrix}x-2\ne0\\x-2\notin Z-\end{matrix}\right.\)\(\Leftrightarrow x\in\left\{3;4;5;6;7;8;9;....n\right\}\)
( Z- là tập hợp số nguyên âm )
Để A có giá trị nguyên thì :
\(\left\{{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
29 tháng 4 2017
a)
2x-3=0 => x=3/2
b)
2x^2 +1 =0 => vô nghiệm
c) x^2 -25 =0 => x=5 loiaj
x=-5 nhân
d)
x^2 -25 =0 => x=5 loại
x=-5 loại
8 tháng 12 2021
a: \(B=\dfrac{x^2-1-2x+3x+1}{x\left(x-1\right)}=\dfrac{x^2+x}{x\left(x-1\right)}=\dfrac{x+1}{x-1}\)
8 tháng 12 2021
a) B = \(\dfrac{x+1}{x}-\dfrac{2}{x-1}+\dfrac{3x+1}{x\left(x-1\right)}\) (ĐK: \(x\ne0;1\))
= \(\dfrac{\left(x+1\right)\left(x-1\right)}{x\left(x-1\right)}-\dfrac{2x}{x\left(x-1\right)}+\dfrac{3x+1}{x\left(x-1\right)}\)
= \(\dfrac{x^2-1-2x+3x+1}{x\left(x-1\right)}=\dfrac{x^2+x}{x\left(x-1\right)}=\dfrac{x+1}{x-1}\)
b) \(\left|x\right|=1< =>\left[{}\begin{matrix}x=1\left(L\right)\\x=-1\left(C\right)\end{matrix}\right.\)
Thay x = -1 vào B, ta có:
\(\dfrac{-1+1}{-1-1}=0\)
c) B nguyên <=> \(\dfrac{x+1}{x-1}\) nguyên <=> \(1+\dfrac{2}{x-1}\) nguyên
<=> 2\(⋮x-1\)
<=> x-1 \(\in\left\{-2;-1;1;2\right\}\)
| x-1 | -2 | -1 | 1 | 2 |
| x | -1 | 0 | 2 | 3 |
| C | L | C | C |
KL: x \(\in\left\{-1;2;3\right\}\)
DM
11 tháng 2 2017
\(A=\frac{2x-y}{3x-y}+\frac{5y-x}{3x+y}\)
\(=\frac{\left(2x-y\right)\left(3x+y\right)+\left(5y-x\right)\left(3x-y\right)}{\left(3x-y\right)\left(3x+y\right)}\)
\(=\frac{3x^2+15xy-6y^2}{9x^2-y^2}\)
\(=\frac{3\left(x^2+5xy-2y^2\right)}{9x^2-y^2}\)
\(=\frac{3\left(10x^2+5xy-3y^2-9x^2+y^2\right)}{9x^2-y^2}\)
\(=-\frac{3\left(9x^2-y^2\right)}{9x^2-y^2}\)
= - 3 (đpcm)
~~~
\(A=\frac{1}{x}+\frac{1}{x+2}+\frac{x-2}{x^2+2x}\)
\(=\frac{x+2+x+x-2}{x^2+2x}\)
\(=\frac{3x}{x\left(x+2\right)}\)
\(=\frac{3}{x+2}\)
\(A\in Z\)
\(\Leftrightarrow3⋮x+2\)
\(\Leftrightarrow x+2\in\text{Ư}\left(3\right)=\left\{-3:-1;1;3\right\}\)
\(\Leftrightarrow x\in\left\{-5;-3;-1;1\right\}\)