
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



3x-3-5 chia het cho x-1
=>3(x-1)-5 chia het cho x-1
=>x-1 thuoc uoc cua 5
=>x thuộc -4;0;2;6
tick nha!
Ta có : 3x-8 chia hết x-1
=>(3x-3)-5 chia hết cho x-1
=>3(x-1)-5 ______________
Vì 3(x-1) chia hết cho (x-1) => 3(x-1)-5 chia hết cho x-1 <=> 5 chia hết cho x-1
=> x-1 \(\inƯ\left(5\right)\)
=>x-1\(\in\left\{-1;1;-5;5\right\}\)
=>x\(\in\left\{0;2;-4;6\right\}\)
Kết luận

\(x^3-3x^2-3x-1=\left(x-4\right)\left(x^2+x+1\right)+3\)
\(\Rightarrow x^3-3x^2-3x-1\) chia hết \(x^2+x+1\) khi \(3⋮x^2+x+1\)
\(\Rightarrow x^2+x+1=Ư\left(3\right)\) (1)
Mà x nguyên dương \(\Rightarrow x^2+x+1\ge1^2+1+1=3\) (2)
(1);(2) \(\Rightarrow x^2+x+1=3\)
\(\Rightarrow x=1\)

a) Ta có : x - 4 chia hết cho x + 1
=> x + 1 - 5 chia hết cho x + 1
=> 5 chia hết cho x + 1
=> x + 1 thuộc Ư(5) = {-5;-1;1;5}
=> x = {-6;-2;0;4}
b) 3x - 1 chia hết cho x - 4
=> 3x - 12 + 11 chia hết cho x - 4
=> 3(x - 4) + 11 chia hết cho x - 4
=> 11 chia hết cho x - 4
=> x - 4 thuộc Ư(11) = {-11;-1;1;11}
=> x = {-7;3;5;15}
a,x-4 chia hết cho x+1
\(\Rightarrow\)x-(1+3) chia hết cho x+1
Mà x+1 chia hết cho x+1 nên 3 chia hết cho x+1
\(\Rightarrow\)x thuộc Ư(3)={1;3}
\(\Rightarrow\)x thuộc {0;2}

Do \(3x-1⋮y\) và \(3y+1⋮x\)nên \(\left(3x-1\right)\left(3y+1\right)⋮xy\)
\(\Rightarrow9xy+3x+3y+1⋮xy\)
Mà \(9xy⋮xy\)
\(\Rightarrow\frac{3x}{y}+3+y\frac{1}{y}⋮x\)
Do vai trò của x , y như nhau , nên giả sử
\(\Rightarrow\frac{x}{y}\le1\)
\(\Rightarrow\frac{3x}{y}+3+\frac{1}{y}< 7\)
\(\Rightarrow1< x< 7\)
\(\Rightarrow x=2;3;4;5;6\)
Thay x vào 3x + 1 \(⋮\)y và 3y-1\(⋮x\)

x^3+3x-5 chia hết cho x^2+2
=>x^3+2x+x-5 chia hết cho x^2+2
=>x-5 chia hết cho x^2+2
=>x^2-25 chia hết cho x^2+2
=>x^2+2-27 chia hết cho x^2+2
=>x^2+2 thuộc Ư(-27)
=>x^2+2 thuộc {3;9;27}
=>\(x\in\left\{1;-1;5;-5\right\}\)

Vì x,y là số nguyên dương mà \(x+1⋮y\)nên \(x+1\ge y\)(1)
Suy ra \(x+3\ge y+2\)(1)
Mặt khác \(y+2⋮x\)nên \(y+2\ge x\)(2)
Từ (1) và (2) suy ra \(x\le y+2\le x+3\)
Suy ra \(y+2=x\)hoặc \(y+2=x+1\)hoặc \(y+2=x+2\)hoặc \(y+2=x+3\)
+Với \(y+2=x\)mà \(x+1⋮y\)nên \(3⋮y\)mà y là số nguyên dương nên y = 1 hoặc y = 3
Nếu y = 1 thì x =3 ( thoả mãn )
Nếu y = 3 thì x = 5 ( thoả mãn )
+ Với \(y+2=x+1\)mà \(x+1⋮y\)nên \(y+2⋮y\)nên \(2⋮y\)mà y là số nguyên dương nên y =1 hoặc y =2
Nếu y =1 thì x = 2 ( không thoả mãn )
Nếu y = 2 thì x =3 ( không thoả mãn )
+Với \(y+2=x+2\)mà \(y+2⋮x\)nên \(y+2⋮y\)nên \(2⋮y\)mà y là số nguyên dương nên y = 1 hoặc y =2
Nếu y = 1 thì x= 1 ( thoả mãn )
Nếu y =2 thì x = 2 ( không thoả mãn )
+Với \(y+2=x+3\)mà \(y+2⋮x\)nên \(x+3⋮x\)nên \(3⋮x\)mà x là số nguyên dương nên x =1 hoặc x = 3
Nếu x = 1 thì y = 2 ( thoả mãn )
Nếu x = 3 thì y = 4 ( thoả mãn )
Kết luận....
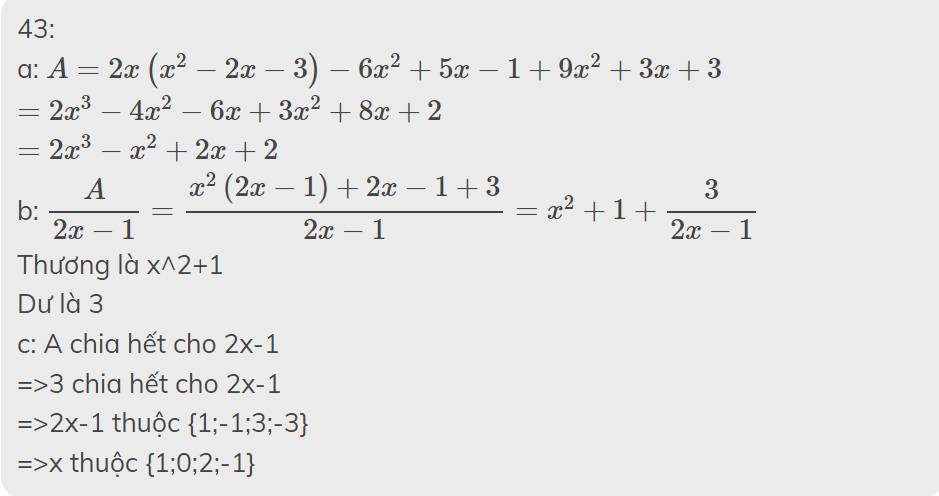
Để 3x-4\(⋮\)x-1
\(\Rightarrow3\left(x-1\right)-1⋮x-1\)
\(\Rightarrow-1⋮x-1\)
\(\Rightarrow x-1\in\left\{1;-1\right\}\)
\(\Rightarrow x\in\left\{2;0\right\}\)
để 3x - 4 chia hết cho x - 1
3 ( x - 1 ) - 1 chia hết cho x - 1
- 1 chia hết cho x - 1
x - 1 thuộc { 1 , - 1 }
x thuộc { 2 , 0 }