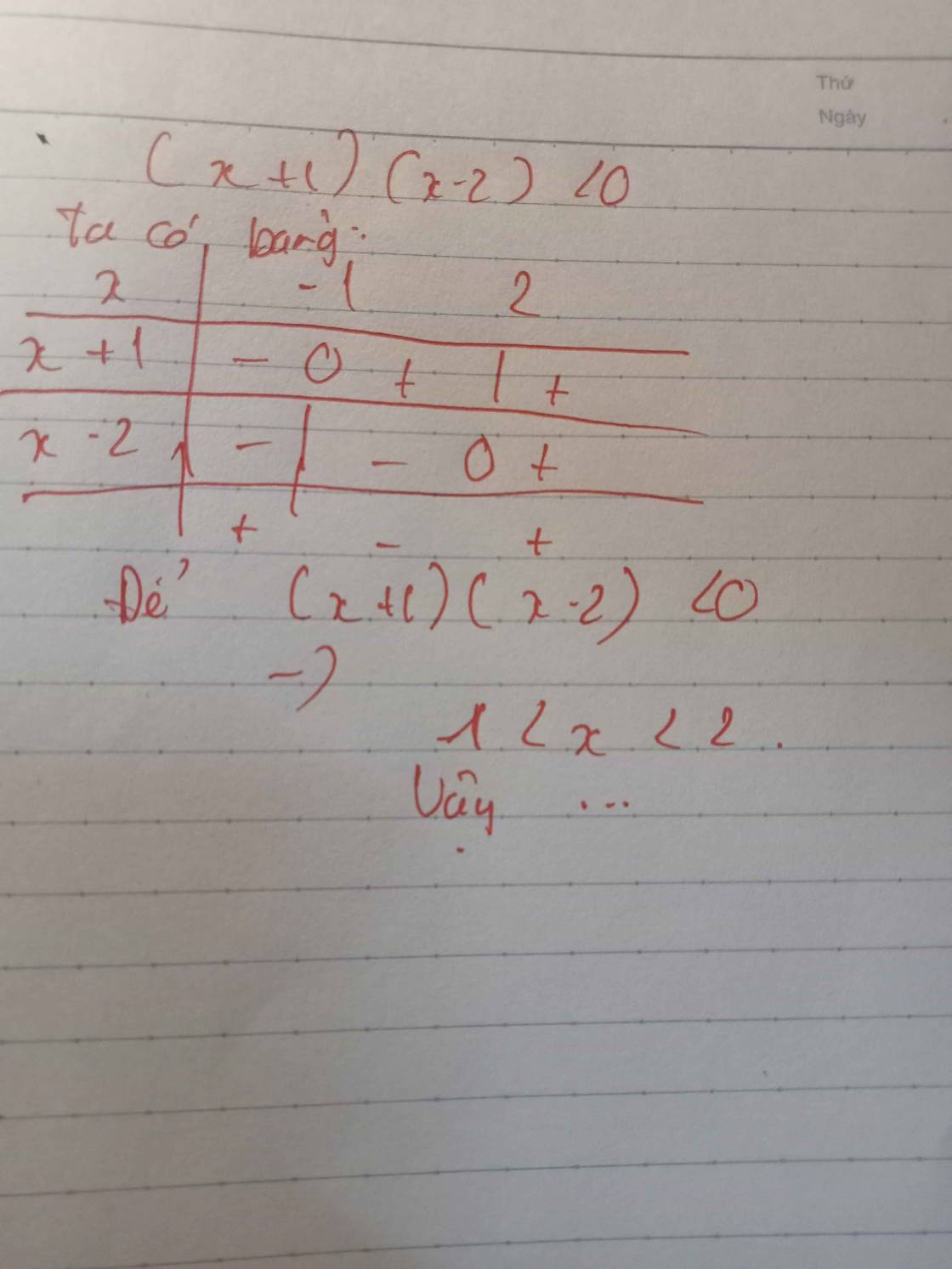Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2+\left(x-1\right)^2=0\)
\(\left(x-1\right)^2=-2\left(loại\right)\)
P/s : làm từng phần một
( x - 1 ) ( x - 5 ) > 0
TH1: cả x - 1 và x - 5 lớn hơn 0
+) x - 1 > 0 => x > 1
+) x - 5 > 0 => x > 5
=> x > 5
TH2 : cả x - 1 và x - 5 đều bé hơn 0
+) x - 1 < 0 => x < 1
+) x - 5 < 0 => x < 5
=> x < 1
Vậy,..........

1)Tìm x
a) (x+1)(x-2)<0
=>Có 2TH:
TH1:
x+1<0=>x< -1
x-2>0=>x>2
=>Vô lí
TH2:
x+1>0=>x> -1
x-2<0=>x<2
=> -1<x<2
Vậy x thuộc {0;1}
b) Tương tự a thôi ạ.
c) (x-2)(3x+2)
=> Có hai TH:
TH1:
x-2<0=>x<2
3x+2<0=>3x< -2=>x< -2/3
=>x< -2/3
TH2:
x-2>0=>x>2
3x+2>0=>3x> -2=>x> -2/3
=>x>2
Vậy x< -2/3 hoặc x>2
2)Tìm x
x.x=x
<=>x²-x=0
<=>x(x-1)=0
<=>x=0 hoặc x=1

\((x+1)x-2(x+1)<0\\\Rightarrow (x+1)(x-2)<0\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+1>0\\x-2< 0\end{matrix}\right.\\\left\{{}\begin{matrix}x+1< 0\\x-2>0\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>-1\\x< 2\end{matrix}\right.\\\left\{{}\begin{matrix}x< -1\\x>2\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}-1< x< 2\\\left\{{}\begin{matrix}x< -1\\x>2\end{matrix}\right.\left(vô.lí\right)\end{matrix}\right.\)
\(\Rightarrow-1< x< 2\)
#\(Toru\)

B1: Đk: 5x ≥ 0 => x ≥ 0
Vì |x + 1| ≥ 0 => |x + 1| = x + 1
|x + 2| ≥ 0 => |x + 2| = x + 2
|x + 3| ≥ 0 => |x + 3| = x + 3
|x + 4| ≥ 0 => |x + 4| = x + 4
=> |x + 1| + |x + 2| + |x + 3| + |x + 4| = 5x
=> x + 1 + x + 2 + x + 3 + x + 4 = 5x
=> 4x + 10 = 5x
=> x = 10
B2: Ta có: |x - 2018| = |2018 - x|
=> A=|x + 2000| + |2018 - x| ≥ |x + 2000 + 2018 - x| = |4018| = 4018
Dấu " = " xảy ra <=> (x + 2000)(x - 2018) ≥ 0
Th1: \(\hept{\begin{cases}x+2000\ge0\\x-2018\ge0\end{cases}\Rightarrow}\hept{\begin{cases}x\ge-2018\\x\le2018\end{cases}}\Rightarrow-2018\le x\le2018\)
Th2: \(\hept{\begin{cases}x+2000\le0\\x-2018\le0\end{cases}\Rightarrow}\hept{\begin{cases}x\le-2018\\x\ge2018\end{cases}}\)(vô lý)
Vậy GTNN của A = 4018 khi -2018 ≤ x ≤ 2018
B3:
a, Vì |x + 1| ≥ 0 ; |2y - 4| ≥ 0
=> |x + 1| + |2y - 4| ≥ 0
Dấu " = " xảy ra <=> \(\hept{\begin{cases}x+1=0\\2y-4=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-1\\y=2\end{cases}}\)
Vậy...
b, Vì |x - y + 1| ≥ 0 ; (y - 3)2 ≥ 0
=> |x - y + 1| + (y - 3)2 ≥ 0
Dấu " = " xảy ra <=> \(\hept{\begin{cases}x-y+1=0\\y-3=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x-y=-1\\y=3\end{cases}}\Leftrightarrow\hept{\begin{cases}x-3=-1\\y=3\end{cases}\Leftrightarrow}\hept{\begin{cases}x=2\\y=3\end{cases}}\)
Vậy...
c, Vì |x + y| ≥ 0 ; |x - z| ≥ 0 ; |2x - 1| ≥ 0
=> |x + y| + |x - z| + |2x - 1| ≥ 0
Dấu " = " xảy ra <=> \(\hept{\begin{cases}x+y=0\\x-z=0\\2x-1=0\end{cases}\Leftrightarrow\hept{\begin{cases}x+y=0\\x=z\\x=\frac{1}{2}\end{cases}\Leftrightarrow}}\hept{\begin{cases}\frac{1}{2}+y=0\\x=z=\frac{1}{2}\end{cases}\Leftrightarrow}\hept{\begin{cases}y=\frac{-1}{2}\\x=z=\frac{1}{2}\end{cases}}\)

Ta có : \(\left|x+3\right|.\left(x^2+1\right)=0\)
<=> |x + 3| = 0 (vì x2 + 1 lớn hơn 0)
=> x + 3 = 0
<=> x = -3

Ta có : \(\dfrac{\left(x-3\right)\left(x+2\right)\left(x+1\right)}{\left(x+3\right)\left(x-4\right)}>0\)
- Đặt \(f\left(x\right)=\dfrac{\left(x-3\right)\left(x+2\right)\left(x+1\right)}{\left(x+3\right)\left(x-4\right)}\)
- Lập bảng xét dấu :
- Từ bảng xét dấu : - Để f(x) > 0
\(\Leftrightarrow\left[{}\begin{matrix}-3< x< -2\\-1< x< 3\\x>4\end{matrix}\right.\)
Vậy ...