K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 1 2022
a: =>(x+10)(x-1)=0
=>x=-10 hoặc x=1
b: \(A=x^3-1-\left(x+5\right)\left(x^2-3\right)-5x^2-10x-5\)
\(=x^3-5x^2-10x-6-x^3+3x-5x^2+15\)
=-7x+9
=110/13
PT
0
Bài 1.
HL
3
27 tháng 9 2020
(x + 2)2 - (x - 1)(x + 1) = 13
=> (x2 + 2.x.2 + 22 )- (x2 - 1) = 13 ( dùng hẳng đẳng thức số 1 và số 3)
=> x2 + 4x + 4 - x2 + 1 = 13
=> (x2 - x2) + 4x + 4 + 1 = 13
=> 4x + 4 + 1 = 13
=> 4x + 5 = 13
=> 4x = 8
=> x = 2
Vậy x = 2
(x + 1)3 + x(x - 1) = x3 + 4x2
=> x3 + 3.x2.1 + 3.x.12 + 13 + x2 - x - x3 - 4x2 = 0
=> x3 + 3x2 + 3x + 1 + x2 - x - x3 - 4x2 = 0
=> (x3 - x3) + (3x2 + x2 - 4x2) + (3x - x) + 1 = 0
=> 2x + 1 = 0 => 2x = -1 => x = -1/2
(x + 1)(x + 2) - (x + 3)2 = 24
=> x(x + 2) + 1(x + 2) - (x2 + 2.x.3 + 32) = 24
=> x2 + 2x + x + 2 - (x2 + 6x + 9) = 24
=> x2 + 2x + x + 2 - x2 - 6x - 9 = 24
=> (x2 - x2) + (2x + x - 6x) + (2 - 9) = 24
=> -3x - 7 = 24
=> -3x = 31
=> x = -31/3
(x - 1)(x2 + x + 1) + 2x = x3 + 5
Dựa vào hằng đẳng thức : (A - B)(A2 + AB + B2) = A3 - B3
=> (x - 1)(x2 + x.1 + 12) = x3 - 13 = x3 - 1
=> x3 - 1 + 2x - x3 - 5 = 0
=> (x3 - x3) - 1 + 2x - 5 = 0
=> -1 + 2x - 5 = 0
=> -1 + 2x = 5
=> 2x = 6
=> x = 3
F
30 tháng 9 2020
\(\left(x+2\right)^2-\left(x-1\right)\left(x+1\right)=13\)
\(\left(x^2+4x+4\right)-\left(x^2-1\right)=13\)
\(x^2+4x+4-x^2+1=13\)
\(4x+5=13\)
\(4x=8\)
\(x=2\)
b,\(\left(x+1\right)^3+x\left(x-1\right)=x^3+4x^2\)
\(x^3+3x^2+3x+1+x^2-x-x^3-4x^2=0\)
\(2x+1=0\)
\(2x=-1\)
\(x=-\frac{1}{2}\)
1 tháng 10 2021
a) \(\left(5-x\right)\left(x-1\right)=-2x\left(x-1\right)\)
\(\Rightarrow\left(5-x\right)\left(x-1\right)+2x\left(x-1\right)=0\)
\(\Rightarrow\left(x-1\right)\left(5-x+2x\right)=0\)
\(\Rightarrow\left(x-1\right)\left(x+5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-5\end{matrix}\right.\)
b) \(\left(x+3\right)^2-\left(x-13\right)\left(x+13\right)=0\)
\(\Rightarrow x^2+6x+9-x^2+169=0\)
\(\Rightarrow6x=-178\Rightarrow x=-\dfrac{89}{3}\)
NL
0
KN
16 tháng 10 2019
\(\left(x-2\right)\left(x-3\right)\left(x-4\right)\left(x-5\right)+1\)(2)
\(=\left(x-2\right)\left(x-5\right)\left(x-3\right)\left(x-4\right)+1\)
\(=\left(x^2-7x+10\right)\left(x^2-7x+12\right)+1\)(1)
Đặt \(x^2-7x+10=t\)
\(\Rightarrow\left(1\right)=t\left(t+2\right)+1=t^2+2t+1=\left(t+1\right)^2\)
Mà \(x^2-7x+10=t\)nên \(\left(2\right)=\left(x^2-7x+11\right)^2\)
Vậy \(\left(x-2\right)\left(x-3\right)\left(x-4\right)\left(x-5\right)+1\)\(=\left(x^2-7x+11\right)^2\)
KN
16 tháng 10 2019
\(\left(x+1\right)^3-x\left(x-3\right)\left(x+3\right)-6\left(x-1\right)\left(x+2\right)=13\)
\(\Leftrightarrow x^3+3x^2+3x+1-x\left(x^2-9\right)-6\left(x^2+x-2\right)=13\)
\(\Leftrightarrow x^3+3x^2+3x+1-x^3+9x-6x^2-6x+12=13\)
\(\Leftrightarrow-3x^2+6x=0\)
\(\Leftrightarrow-3\left(x^2-2\right)=0\)
\(\Leftrightarrow x^2-2=0\Leftrightarrow x^2=2\)
\(\Leftrightarrow x=\pm\sqrt{2}\)
MT
3
19 tháng 9 2016
\(\frac{x+1}{12}+\frac{x+2}{13}=\frac{x+3}{14}+\frac{x+4}{15}\) .Trừ 1 ở mỗi hạng tử của 2 vế ,ta có :
\(\frac{x-11}{12}+\frac{x-11}{13}=\frac{x-11}{14}+\frac{x-11}{15}\Rightarrow\left(\frac{1}{12}+\frac{1}{13}\right)\left(x-11\right)=\left(\frac{1}{14}+\frac{1}{15}\right)\left(x-11\right)\)
\(\Rightarrow\left[\left(\frac{1}{12}+\frac{1}{13}\right)-\left(\frac{1}{14}+\frac{1}{15}\right)\right]\left(x-11\right)=0\)
\(\frac{1}{12}>\frac{1}{14};\frac{1}{13}>\frac{1}{15}\Rightarrow\frac{1}{12}+\frac{1}{13}>\frac{1}{14}+\frac{1}{15}\Rightarrow\left(\frac{1}{12}+\frac{1}{13}\right)-\left(\frac{1}{14}+\frac{1}{15}\right)\ne0\)
\(\Rightarrow x-11=0\Rightarrow x=11\)
MA
19 tháng 9 2016
\(\frac{x+1}{12}+\frac{x+2}{13}=\frac{x+3}{14}+\frac{x+4}{15}\)
\(\Leftrightarrow\frac{x+1}{12}-1+\frac{x+2}{13}-1=\frac{x+3}{14}-1+\frac{x+4}{15}-1\)
\(\Leftrightarrow\frac{x-11}{12}+\frac{x-11}{13}=\frac{x-11}{14}+\frac{x-11}{15}\)
\(\Leftrightarrow\frac{x-11}{12}+\frac{x-11}{13}-\frac{x-11}{14}-\frac{x-11}{15}=0\)
\(\Leftrightarrow\left(x-11\right)\left(\frac{1}{12}+\frac{1}{13}-\frac{1}{14}-\frac{1}{15}\right)=0\)
Mà: \(\frac{1}{12}+\frac{1}{13}-\frac{1}{14}-\frac{1}{15}\ne0\)
\(\Rightarrow x-11=0\Rightarrow x=11\)
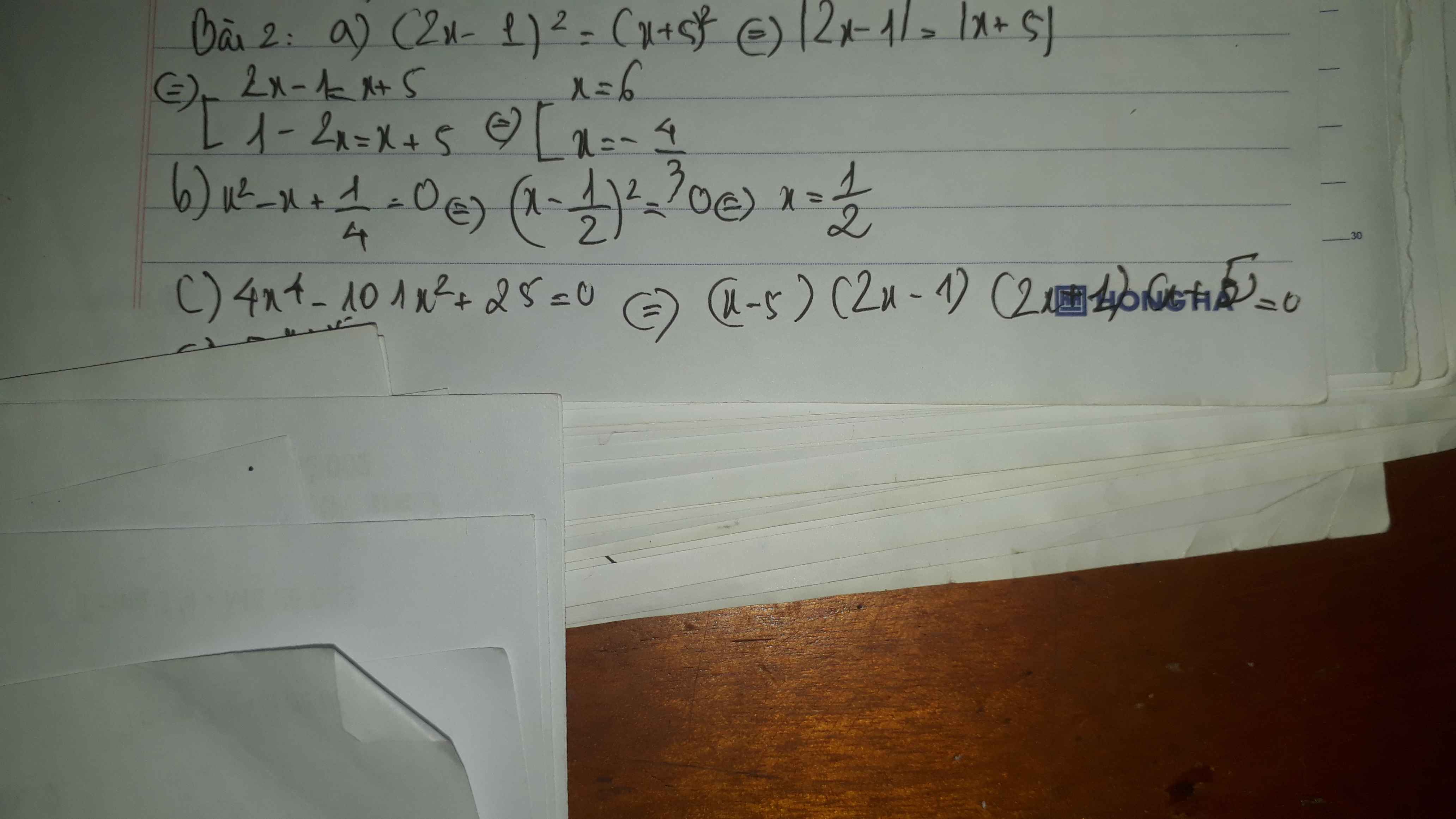
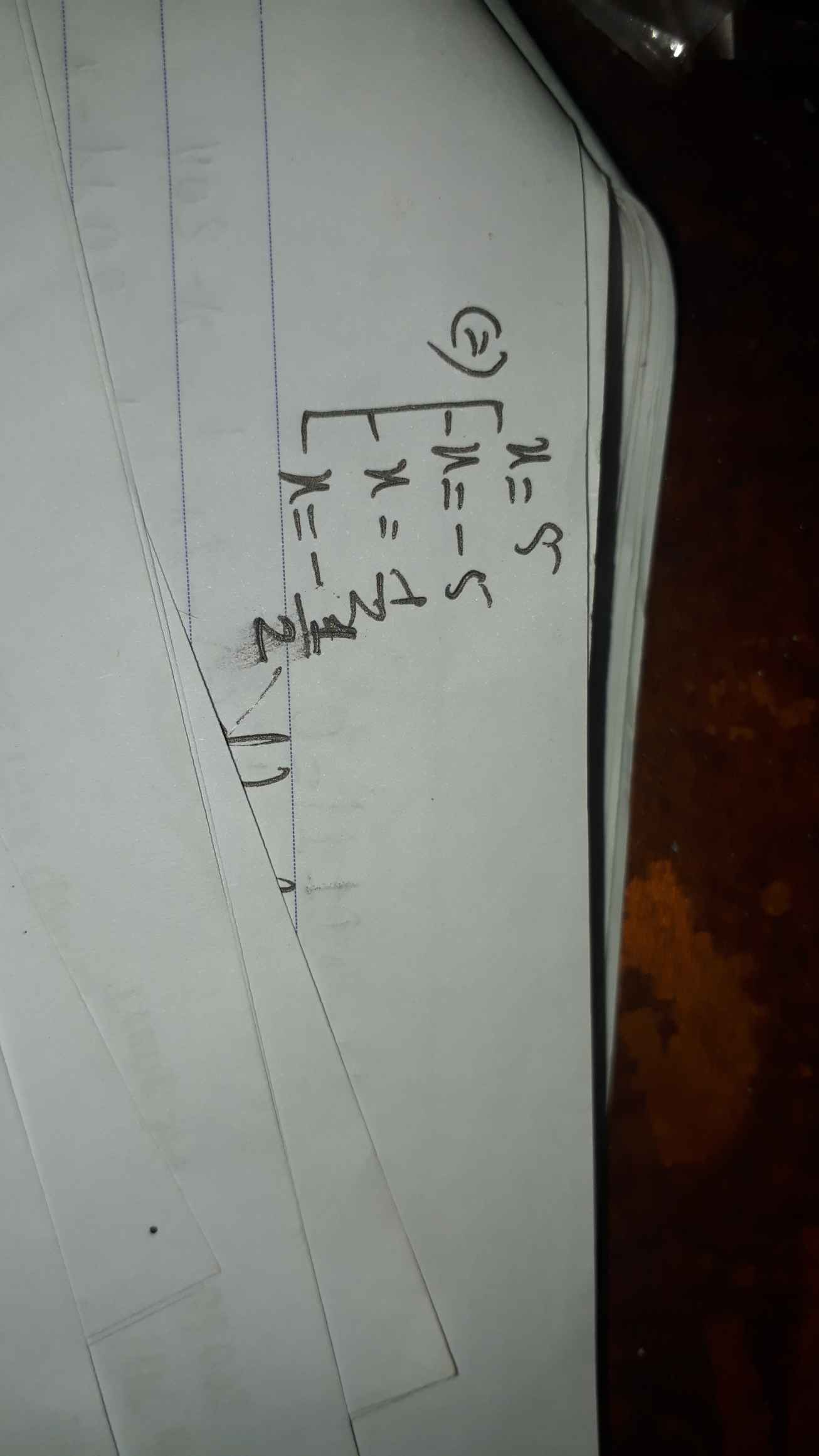
\(x\left(x-2\right)+\left(1-x\right)\left(1+x\right)=13\\ =>x^2-2x+1-x^2-13=0\\ =>-2x-12=0\\ =>-2x=12\\ =>x=12:\left(-2\right)\\ =>x=-6\)
Vậy \(x=-6\)
x( x-2) + ( 1 - x)(1+x) = 13
x2- 2x + 1 - x2 = 13
-2 x = 12
x = 12 : (-2)
x = - 6