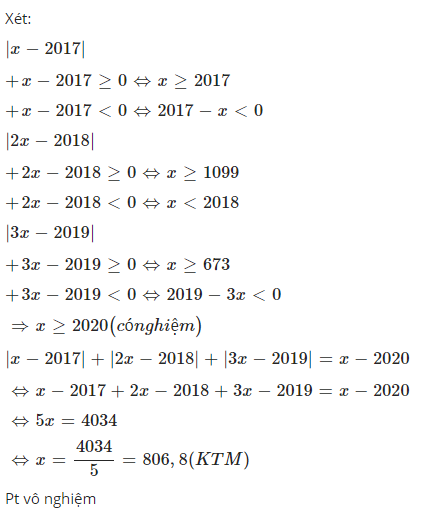Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Nhận thấy vế trái luôn dương nên \(x-2020\ge0\Leftrightarrow x\ge2020\)
Với \(x\ge2020\Rightarrow\left\{{}\begin{matrix}x-2017\ge0\\2x-2018\ge0\\3x-2019\ge0\end{matrix}\right.\)
PT trở thành: \(x-2017+2x-2018+3x-2019=x-2020\)
Hay kết hợp với điều kiện \(x=\dfrac{4034}{5}\) suy ra PT đã cho vô nghiệm

a,\(x^5-x^4-x^4+x^3+2x^3-2x^2-2x^2+2\)2x-2x+2\(x^4\left(x-1\right)-x^3\left(x-1\right)+2x^2\left(x-1\right)-2x\left(x-1\right)+2\left(x-1\right)\)
=\(\left(x^4-x^3+2x^2-2x+2\right)\left(x-1\right)\)
b,


ta co (2x-1)(3x+1)+(3x+4)(3-2x)=5
(=)6x2-3x+2x-1+6x-6x2+12-8x=5
(=)-4x+11=5
(=)-4x=-6
(=)x=3/2
(2x-1)(3x+1)+(3x-4)(3-2x)=5
<=> 6x2+2x-3x-1+9x-6x2-12+8x=5
<=> 16x-13=5
<=> 16x = 18
<=> x=9/8