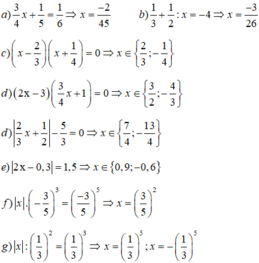CT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KD
15 tháng 8 2018
\(\left|x-3,2\right|+\left|2x-\frac{1}{5}\right|=x+3.\)
ĐK : \(x+3\ge0\Leftrightarrow x\ge-3\)
Th1 : \(x-3,2+2x-\frac{1}{5}=x+3\)
\(x-3,2+2x=x+\frac{16}{5}\)
\(x+2x=x+\frac{32}{5}\)
\(2x=\frac{32}{5}\)
\(\Leftrightarrow x=3,2\)(tm)
\(x-3,2+2x-\frac{1}{5}=3-x\)
\(x-3,2+2x=3-x+\frac{1}{5}\)
\(x-3,2+2x=\frac{16}{5}-x\)
\(x+2x=\frac{16}{5}-x+3,2\)
\(x+2x=\frac{32}{5}-x\)
\(2x=\frac{32}{5}-x-x\)
\(2x=\frac{32}{5}-2x\)
\(4x=\frac{32}{5}\)
\(x=1,6\)(tm)
Vậy \(x=1,6\)hoặc \(x=3,2\)
TH
2
25 tháng 8 2023
1)
xy + x - 4y = 12
x + y(x - 4) = 12
y(x - 4) = 12 - x
\(y=\dfrac{-x+12}{x-4}\)
Vì \(x,y\inℕ\) nên
\(\left(-x+12\right)⋮\left(x-4\right)\)
\(\left(-x+12\right)-\left(x-4\right)⋮\left(x-4\right)\)
\(16⋮\left(x-4\right)\)
\(\left(x-4\right)\inƯ\left(16\right)\)
\(\left(x-4\right)\in\left\{1;-1;2;-2;4;-4;8;-8;16;-16\right\}\)
\(x\in\left\{5;3;6;2;8;0;12;-4;20;-12\right\}\)
\(y\in\left\{\dfrac{-5+12}{5-4};\dfrac{-3+12}{3-4};\dfrac{-6+12}{6-4};\dfrac{-2+12}{2-4};\dfrac{-8+12}{8-4};\dfrac{-0+12}{0-4};\dfrac{-12+12}{12-4};\dfrac{4+12}{-4-4};\dfrac{-20+12}{20-4};\dfrac{12+12}{-12-4}\right\}\)
\(y\in\left\{7;-9;3;-5;1;-3;0;-2;-\dfrac{1}{2};-\dfrac{7}{5}\right\}\)
\(\left(x;y\right)\in\left\{\left(5;7\right);\left(3;-9\right);\left(6;3\right);\left(2;-5\right);\left(8;1\right);\left(0;-3\right);\left(12;0\right);\left(-4;-2\right);\left(20;-\dfrac{1}{2}\right);\left(-12;-\dfrac{7}{5}\right)\right\}\)
Mà \(x,y\inℕ\) nên các giá trị cần tìm là \(\left(x;y\right)\in\left\{\left(5;7\right);\left(6;3\right);\left(8;1\right);\left(12;0\right)\right\}\)
2)
(2x + 3)(y - 2) = 15
\(\left(2x+3\right)\inƯ\left(15\right)\)
\(\left(2x+3\right)\in\left\{1;-1;3;-3;5;-5;15;-15\right\}\)
Ta lập bảng
| 2x + 3 | 1 | -1 | 3 | -3 | 5 | -5 | 15 | -15 |
| y - 2 | 15 | -15 | 5 | -5 | 3 | -3 | 1 | -1 |
| (x; y) | (-1; 17) | (-2; -13) | (0; 7) | (-3; -3) | (1; 5) | (-4; -1) | (6; 3) | (-9; 1) |
Mà \(x,y\inℕ\) nên các giá trị cần tìm là \(\left(x;y\right)\in\left\{\left(0;7\right);\left(1;5\right);\left(6;3\right)\right\}\)
29 tháng 12 2016
theo mk thì bài của bạn làm kết quả đúng nhưng bn trình bày vẫn chưa đc hợp lí, mỗi bước xuống dòng bn phải có dấu suy ra, kết luận đang còn thiếu, kết luận ko có trừ 0,25 điểm, đặt dấu bằng là sai trừ 0,25 điểm.
M
2
QT
Quoc Tran Anh Le
Giáo viên
4 tháng 7 2019
a) \(\left|x-3,2\right|=1,5\)
\(\Rightarrow x-3,2=\pm1,5\)
\(\Leftrightarrow x=\left\{1,7;4,7\right\}\)
b) \(\left|5x-7\right|=5x-7\)
\(\Rightarrow5x-7=\left[{}\begin{matrix}5x-7\left(x\ge0\right)\\7-5x\left(x< 0\right)\end{matrix}\right.\)
Với \(x\ge0\): \(5x-7=5x-7\)
\(\Rightarrow\) x bất kì
Với \(x< 0\): \(5x-7=7-5x\)
\(\Rightarrow5x-7-7+5x=0\)
\(\Leftrightarrow10x-14=0\)
\(\Leftrightarrow x=\frac{14}{10}\) (không thỏa mãn điều kiện)
Vậy \(x\ge0\).
c) \(\left|2x-3\right|=3-2x\)
\(\Rightarrow2x-3=\left[{}\begin{matrix}3-2x\left(x\ge0\right)\\2x-3\left(x< 0\right)\end{matrix}\right.\)
Với \(x\ge0\): \(2x-3=3-2x\)
\(\Rightarrow2x-3-3+2x=0\)
\(\Leftrightarrow4x-6=0\)
\(\Leftrightarrow x=\frac{6}{4}=\frac{3}{2}\)
Với x < 0: \(2x-3=2x-3\)
\(\Rightarrow\) x bất kì
Vậy \(x< 0\) và \(x=\frac{3}{2}\)
VM
4 tháng 7 2019
a) | x - 3, 2 | = 1, 5
TH1: x - 3, 2 = 1, 5
x = 1, 5 + 3, 2
x = 4, 7.
TH2: x - 3, 2 = -1, 5
x = (-1, 5) + 3, 2
x = 1, 7.
Vậy x ∈ { 4, 7 ; 1, 7}
Mình chỉ làm câu a) thôi nhé.
Chúc bạn học tốt!
ZA
0
AT
1
E
22 tháng 9 2017
Bài này có 2 cách, cách 1 là xét 3 trường hợp, cách 2 là sử dụng phương pháp đánh giá. Trong bài này cách 2 ngắn hơn thì mình sẽ làm.
Điều kiện: x \(\ge\)0
Ta có: VT = |x - 3,2| + |2x - 0,2| = |3,2 - x| + |2x - 0,2| \(\ge\) |3,2 - x + 2x - 0,2| = |x + 3| = VP
Dấu "=" xảy ra <=> (3,2 - x)(2x - 0,2) \(\ge\) 0.
<=> \(\left[{}\begin{matrix}\left\{{}\begin{matrix}3,2-x\ge0\\2x-0,2\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le3,2\\x\ge0,1\end{matrix}\right.\Leftrightarrow0,1\le x\le3,2}}\\\left\{{}\begin{matrix}3,2-x\le0\\2x-0,2\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge3,2\\x\le0,1\end{matrix}\right.\Leftrightarrow x}\in\varphi}\end{matrix}\right.\)
24 tháng 3 2022
a/Ta có: M(x)+N(x) = (2x5 - 4x3 + 2x2 + 10x - 1) + (-2x5 + 2x4 + 4x3 + x2 + x - 10)
= 2x5 - 2x5 - 4x3 + 4x3 + 2x4 + 2x2 + x2 + 10x + x -1 - 10
= 2x4 + 3x2 + 11x - 11
b/ Ta có: A(x) = N(x)-M(x) = (-2x5 + 2x4 + 4x3 + x2 + x - 10) - (2x5 - 4x3 + 2x2 + 10x - 1)
= -2x5 - 2x5 + 2x4 + 4x3 + 4x3 + x2 - 2x2 + x - 10x -10 + 1
= -2x5 + 2x4 + 8x3 - x2 - 9x -9
30 tháng 1 2022
Bài 3:
a: \(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\\dfrac{3}{4}x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{4}{3}\end{matrix}\right.\)
b: \(\Leftrightarrow\left\{{}\begin{matrix}3x+2>0\\\dfrac{2}{3}x-5< 0\end{matrix}\right.\Leftrightarrow-\dfrac{2}{3}< x< \dfrac{15}{2}\)
c: \(\Leftrightarrow\left[{}\begin{matrix}\dfrac{3}{4}x+2=0\\\dfrac{2}{5}x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\cdot\dfrac{3}{4}=-2\\\dfrac{2}{5}x=6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{8}{3}\\x=6:\dfrac{2}{5}=15\end{matrix}\right.\)
