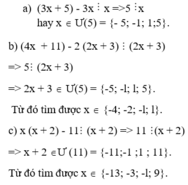Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



15 chia hết cho 2x+ 1 2x + 1 thuộc Ư(15) = {1;3;5;15} 2x + 1 = 1 => x= 0 2x+ 1 = 3 => x= 1 2x + 1 = 5 => x = 2 2x + 1= 15 => x = 7 Vậy x thuộc {0;1;2;7}
a) 15 chia hết cho (2x+1) => 2x+1 thuộc Ư(15)
ta có: Ư(15)={5;3;1;15}
Ta có: 2x+1= 1 thì x=0
Nếu 2x+1=3 thì x= 1
Nếu 2x+1=5 thì x=3
Nếu 2x+1=15 thì x= 7
b) 10 chia hết cho 3x+1 => 3x+1 thuộc Ư(10)
Ta có: Ư(10)={1;5;2;10}
| 1 | 5 | 2 | 10 | |
| x | loại | loại | 1 | 3 |
c) Vì x+16 chia hết cho x+1
=> (x+1)+15 chia hết cho x+1
Vì x+1 chia hết cho x+1 => 15 chia hết cho x+1
bạn làm theo cách tương tự như câu a nhé
d) Ta có: x+11 chia hết cho x+1
=> (x+1)+10 chia hết cho x+1
Vì x+1 chia hết cho x+1 => 10 chia hết cho x+1
bạn làm tương tự như câu b nhé

a: \(\Leftrightarrow6x+8⋮2x-11\)
\(\Leftrightarrow2x-11\in\left\{1;-1;41;-41\right\}\)
hay \(x\in\left\{6;5;26;-15\right\}\)
b: \(\Leftrightarrow x^2-4-5⋮x-2\)
\(\Leftrightarrow x-2\in\left\{1;-1;5;-5\right\}\)
hay \(x\in\left\{3;1;7;-3\right\}\)
c: \(\Leftrightarrow3x-6+9⋮x-2\)
\(\Leftrightarrow x-2\in\left\{1;-1;3;-3;9;-9\right\}\)
hay \(x\in\left\{3;1;5;-1;11;-7\right\}\)

+) 11 - 2x luôn chia hết 11 - 2x
=> 3.(11 - 2x) chia hết cho 11 - 2x hay 33 - 6x chia hết cho 11 - 2x
+) 3x + 1 chia hết cho 11 - 2x => 2.(3x+ 1) chia hết cho 11 - 2x Hay 6x + 2 chia hết cho 11 - 2x
=> (33 - 6x) + (6x + 2) chia hết cho 11 - 2x
=> 35 chia hết cho 11 - 2x
=> 11 - 2x \(\in\) Ư(35) = {35;7;5;1}
+) 11 - 2x = 35 => x =....
+﴿ 11 ‐ 2x luôn chia hết 11 ‐ 2x
=> 3.﴾11 ‐ 2x﴿ chia hết cho 11 ‐ 2x hay 33 ‐ 6x chia hết cho 11 ‐ 2x
+﴿ 3x + 1 chia hết cho 11 ‐ 2x => 2.﴾3x+ 1﴿ chia hết cho 11 ‐ 2x Hay 6x + 2 chia hết cho 11 ‐ 2x
=> ﴾33 ‐ 6x﴿ + ﴾6x + 2﴿ chia hết cho 11 ‐ 2x
=> 35 chia hết cho 11 ‐ 2x => 11 ‐ 2x \﴾\in\﴿ Ư﴾35﴿ = {35;7;5;1}
+﴿ 11 ‐ 2x = 35 => x =35;7;5;1

\(a,2x+1⋮x-2\)
\(=>2.\left(x-2\right)+5⋮x-2\)
Do \(2.\left(x-2\right)⋮x-2\)
\(=>5⋮x-2\)
\(=>x-2\inƯ\left(5\right)\)
Nên ta có bảng sau :
| x-2 | 1 | 5 | -1 | -5 |
| x | 3 | 7 | 1 | -3 |
Vậy ...
\(b,3x+5⋮x\)
Do \(3x⋮x=>5⋮x\)
\(=>x\inƯ\left(5\right)\)
Nên ta có bảng sau :
| x | 1 | 5 | -1 | -5 |
Vậy ...
\(c,4x+1⋮2x+3\)
\(=>2.\left(2x+3\right)-5⋮2x+3\)
Do \(2.\left(2x+3\right)⋮2x+3\)
\(=>5⋮2x+3\)
\(=>2x+3\inƯ\left(5\right)\)
Nên ta có bảng sau :
| 2x+3 | 1 | 5 | -1 | -5 |
| 2x | -2 | 2 | -4 | -8 |
| x | -1 | 1 | -2 | -4 |
Vậy ...
a) Ta có: 2x+1=2(x-2)+5
Để 2x+1 chia hết cho x-2 thì 2(x-2)+5 chia hết cho x-2
Vì 2(x-2) chia hết cho x-2
=> 5 chia hết cho x-2
Vì x thuộc Z => z-2 thuộc Ư (5)={-5;-1;1;5}
Nếu x-2=-5 => x=-3
Nếu x-2=-1 => x=1
Nếu x-2=1 => x=3
Nếu x-1=5 => x=6
b) Ta có 3x chia hết cho x với mọi x
=> Để 3x+5 chia hết cho x thì 5 chia hết cho x
Vì x thuộc Z => x thuộc Ư (5)={-5;-1;1;5}
c) Ta có: 4x+11=2(2x+3)+5
Để 4x+11 chia hết cho 2x+3 thì 2(2x+3)+5 chia hết cho 2x+3
Vì 2(2x+3) chia hết cho 2x+3 => 5 chia hết cho 2x+3
Vì x thuộc Z => 2x+3 thuộc Ư (5)={-5;-1;1;5}
Nếu 2x+3=-5 => 2x=-8 => x=-4
Nếu 2x+3=-1 => 2x=-4 => x=-2
Nếu 2x+3=1 => 2x=-2 => x=-1
Nếu 2x+3=5 => 2x=2 => x=1