
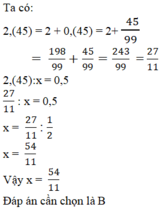
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

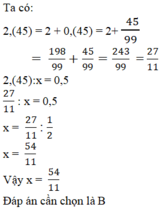

a) => \(\left(\frac{1}{3}-\frac{5}{6}x\right)^3=\frac{5}{6}-\frac{21}{54}=\frac{24}{54}=\frac{4}{9}\)
=> \(\frac{1}{3}-\frac{5}{6}x=\sqrt[3]{\frac{4}{9}}\) => \(\frac{5}{6}x=\frac{1}{3}-\sqrt[3]{\frac{4}{9}}\) => \(x=\frac{6}{5}.\left(\frac{1}{3}-\sqrt[3]{\frac{4}{9}}\right)\)
b) \(\frac{1}{3}\left(\frac{1}{2}x-1\right)^4=\frac{1}{12}-\frac{1}{16}=\frac{1}{48}\) => \(\left(\frac{1}{2}x-1\right)^4=\frac{3}{48}=\frac{1}{16}\)
=> \(\frac{1}{2}x-1=\frac{1}{2}\) hoặc \(\frac{1}{2}x-1=-\frac{1}{2}\)
=> \(\frac{1}{2}x=\frac{3}{2}\) hoặc \(\frac{1}{2}x=\frac{1}{2}\) => x = 3 hoặc x = 1
c) \(\left(1+5\right).\left(\frac{3}{5}\right)^{x-1}=\frac{54}{25}\) => \(\left(\frac{3}{5}\right)^{x-1}=\frac{9}{25}=\left(\frac{3}{5}\right)^2\)
=> x - 1= 2 => x = 3
d) \(\left(1+\left(\frac{2}{3}\right)^2\right).\left(\frac{2}{3}\right)^x=\frac{101}{243}\) => \(\frac{13}{9}.\left(\frac{2}{3}\right)^x=\frac{101}{243}\)
=> \(\left(\frac{2}{3}\right)^x=\frac{101}{243}:\frac{13}{9}=\frac{101}{351}\) (có lẽ đề sai)
2) \(\frac{1}{27^{11}}=\frac{1}{\left(3^3\right)^{11}}=\frac{1}{3^{33}}\); \(\frac{1}{81^8}=\frac{1}{\left(3^4\right)^8}=\frac{1}{3^{32}}\)
Vì 333 > 332 => \(\frac{1}{3^{33}}\) < \(\frac{1}{3^{32}}\) => \(\frac{1}{27^{11}}\) < \(\frac{1}{81^8}\)
b) \(\frac{1}{3^{99}}=\frac{1}{\left(3^3\right)^{33}}=\frac{1}{27^{33}}

\(1,\\ \left(x-7\right)^{x+1}-\left(x-7\right)^{x+11}=0\\ \Leftrightarrow\left(x-7\right)^{x+1}\left[1-\left(x-7\right)^{10}\right]=0\\ \Leftrightarrow\left[{}\begin{matrix}\left(x-7\right)^{x+1}=0\\\left(x-7\right)^{10}=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-7=0\\x-7=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=7\\x=8\end{matrix}\right.\)
\(2,\\ a,\left|2x-3\right|>5\Leftrightarrow\left[{}\begin{matrix}2x-3< -5\\2x-3>5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x< -1\\x>4\end{matrix}\right.\\ b,\left|3x-1\right|\le7\Leftrightarrow\left[{}\begin{matrix}3x-1\le7\\1-3x\le7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\le\dfrac{8}{3}\\x\ge-2\end{matrix}\right.\\ c,\cdot x< -\dfrac{3}{2}\\ \Leftrightarrow5-3x+\left(-2x-3\right)=7\Leftrightarrow2-5x=7\Leftrightarrow x=-1\left(ktm\right)\\ \cdot-\dfrac{3}{2}\le x\le\dfrac{5}{3}\\ \Leftrightarrow\left(5-3x\right)+\left(2x+3\right)=7\Leftrightarrow8-x=7\Leftrightarrow x=1\left(tm\right)\\ \cdot x>\dfrac{5}{3}\\ \Leftrightarrow\left(3x-5\right)+\left(2x+3\right)=7\Leftrightarrow5x-2=7\Leftrightarrow x=\dfrac{9}{5}\left(tm\right)\\ \Leftrightarrow S=\left\{1;\dfrac{9}{5}\right\}\)

a) x : 11 = y : 7
=> x/7 = y/11 và x + y = -54 Thay vào ta có :
x/7 = y/11 = (x+y)/(7+11) = -54/18= -3
=> x = -3.7 = -27
=> y = -3.11 = -33

b) \(\frac{x-99}{5}+\frac{x-97}{7}=\frac{x-95}{9}+\frac{x-93}{11}\)
\(\Leftrightarrow\left(\frac{x-99}{5}-1\right)+\left(\frac{x-97}{7}-1\right)=\left(\frac{x-95}{9}-1\right)\)\(+\left(\frac{x-93}{11}-1\right)\)
\(\Leftrightarrow\frac{x-104}{5}+\frac{x-104}{7}-\frac{x-104}{9}-\frac{x-104}{11}=0\)
\(\Leftrightarrow\left(x-104\right)\left(\frac{1}{5}+\frac{1}{7}-\frac{1}{9}-\frac{1}{11}\right)=0\)
Mà \(\frac{1}{5}+\frac{1}{7}-\frac{1}{9}-\frac{1}{11}\ne0\)
\(\Rightarrow x-104=0\)
\(\Leftrightarrow x=104\)
Vậy ....
a) \(\frac{x+1945}{45}+\frac{x+1954}{54}=\frac{x+1975}{75}+\frac{x+1969}{69}\)
\(\Leftrightarrow\left(\frac{x+1945}{45}-1\right)+\left(\frac{x+1954}{54}-1\right)=\left(\frac{x+1975}{75}-1\right)\)\(+\left(\frac{x+1969}{69}-1\right)\)
\(\Leftrightarrow\frac{x+1900}{45}+\frac{x+1900}{54}-\frac{x+1900}{75}-\frac{x+1900}{69}=0\)
\(\Leftrightarrow\left(x+1900\right)\left(\frac{1}{45}+\frac{1}{54}-\frac{1}{75}-\frac{1}{69}\right)=0\)
Mà \(\frac{1}{45}+\frac{1}{54}-\frac{1}{75}-\frac{1}{69}\ne0\)
\(\Rightarrow x+1900=0\)
\(\Leftrightarrow x=-1900\)
Vậy ...

2) a) \(\frac{1}{27^{11}}=\frac{1}{\left(3^3\right)^{11}}=\frac{1}{3^{33}}\)
\(\frac{21}{81^8}=\frac{21}{\left(3^4\right)^8}=\frac{21}{3^{32}}=\frac{21.3}{3^{33}}=\frac{63}{3^{33}}>\frac{1}{3^{33}}\)
=> \(\frac{21}{81^8}>\frac{1}{27^{11}}\)
b) Rõ ràng : 399 < 1121 => \(\frac{1}{399}>\frac{1}{11^{21}}\)
a) \(\left(\frac{1}{3}-\frac{5}{6}x\right)^3=\frac{5}{6}-\frac{21}{54}\)=> \(\left(\frac{1}{3}-\frac{5}{6}x\right)^3=\frac{24}{54}=\frac{4}{9}\)
=> \(\frac{1}{3}-\frac{5}{6}x=\sqrt[3]{\frac{4}{9}}\) => \(\frac{5}{6}x=1-\sqrt[3]{\frac{4}{9}}\)
=> x = \(\frac{6}{5}-\frac{6}{5}.\sqrt[3]{\frac{4}{9}}\)
b) => \(\frac{1}{13}\left(\frac{1}{2}x-1\right)^4=\frac{1}{12}-\frac{1}{16}=\frac{1}{48}\)
=> \(\left(\frac{1}{2}x-1\right)^4=\frac{13}{48}\)
=> \(\frac{1}{2}x-1=\sqrt[4]{\frac{13}{48}}\) hoặc \(\frac{1}{2}x-1=-\sqrt[4]{\frac{13}{48}}\)
=> \(x=2+2\sqrt[4]{\frac{13}{48}}\) hoặc \(x=2-2\sqrt[4]{\frac{13}{48}}\)