Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương trình ⇔ − m = x 3 − 12 x − 2 . Điều kiện trở thành đường y= m cắt đồ thị hàm số y = x 3 − 12 x − 2 tại 3 điểm phân biệt.
Lập bảng biến thiên của y = x 3 − 12 x − 2 .
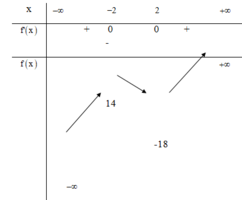
Nhìn vào bảng biến thiên, điều kiện của m là − m ∈ 14 ; − 18 ⇔ m ∈ − 14 ; 18 .

Đáp án C
Phương pháp:
Đặt 2 x = t t > 0 , đưa về phương trình bậc 2 ẩn t, tìm điều kiện của phương trình bậc 2 ẩn t để phương trình ban đầu có 2 nghiệm phân biệt.
Cách giải: Đặt 2 x = t t > 0 khi đó phương trình trở thành t 2 − 2 m t + m + 2 = 0 *
Để phương trình ban đầu có 2 nghiệm phân biệt thì phương trình (*) có 2 nghiệm dương phân biệt.
Khi đó: Δ ' > 0 S > 0 P > 0 ⇔ m 2 − m − 2 > 0 2 m > 0 m + 2 > 0 ⇔ m > 2 m < − 1 m > 0 m > − 2 ⇒ m > 2
Chú ý và sai lầm: Rất nhiều học sinh sau khi đặt ẩn phụ thì quên mất điều kiện t > 0, dẫn đến việc chỉ đi tìm điều kiện đề phương trình (*) có 2 nghiệm phân biệt.

Đáp án D
Phương pháp:
Đánh giá số nghiệm của phương trình f(x) = m + 1 bằng số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m + 1
Cách giải:
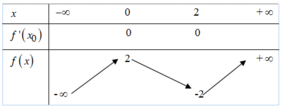
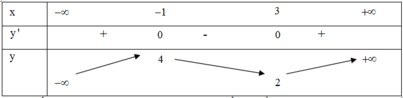
Số nghiệm của phương trình f(x) = m + 1 bằng số giao điểm của đồ thị hàm số y = f(x)
và đường thẳng y = m + 1
Để f(x) = m + 1 có 3 nghiệm thực phân biệt thì –2 < m+1 < 4 ó –3 < m < 3

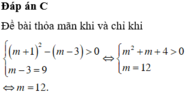




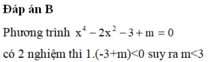
Đáp án B
P T ⇔ x − m x 2 + x m + m 2 − 3 x − m x + m = 0
⇔ x − m x 2 + m x − 3 x + m 2 − 3 m = 0 ⇔ x = m g x = x 2 + m − 3 x + m 2 − 3 m
PT có 3 nghiệm phân biệt ⇔ g x = 0 có 2 nghiệm phân biệt khác m
⇔ Δ = m − 3 2 − 4 m 2 − 3 m > 0 g m = 3 m 2 − 6 m ≠ 0 ⇔ − 3 m 2 + 6 m + 9 > 0 m ≠ 0 ; m ≠ 6 ⇔ − 1 < m < 3 m ≠ 0 ; m ≠ 2