Tìm tất cả các giá trị của tham số m để phương trình x

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

26 tháng 1 2017

Tìm tất cả các giá trị của tham số m để phương trình x - 1 l o g 3 ( x + 1 ) = m có hai nghiệm phân biệt

A. -1 < m ≠ 0

B. m > -1

C. không tồn tại m

D. -1 < m < 0

#Mẫu giáo

Cao Minh Tâm

26 tháng 1 2017

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

ha cam

14 tháng 4 2016

Tìm m để phương trình sau có 3 nghiệm phân biệt:

3x³- 18x² +27x + 3 - 3^1-m =0

#Mẫu giáo

Pham Trong Bach

8 tháng 6 2018

Tìm tất cả các giá trị của tham số m bất phương trình 4 x − 1 − m 2 x + 1 > 0 có nghiệm với x ∈ ℝ A. m ≤ 0 B. m ∈ 0 ; + ∞ C. m ∈ 0 ; 1 D. m ∈ − ∞ ; 0 ∪ 1 ; + ∞ ...

Đọc tiếp

#Mẫu giáo

Cao Minh Tâm

8 tháng 6 2018

Đáp án A

Đặt t = 2 x > 0 ta có t 2 4 − m t + 1 > 0 ⇔ g t = t 2 4 t + 1 > m (do t > 0 )

Bất PT có nghiệm với x ∈ ℝ ⇔ min x > 0 g t > m

Xét g t = 1 4 t 2 t + 1 t > 0 ta có g ' t = 2 t t + 1 − t 2 4 t + 1 2 = t 2 + 2 t 4 t + 1 2 > 0 ∀ t > 0

Do đó hàm số đồng biến trên 0 ; + ∞

Lập BBT suy ra m ≤ 0 là giá trị cần tìm

Đúng(0)

ha cam

14 tháng 4 2016

giaỉ giúp mình:

Tìm m để phương trình sau có 3 nghiệm phân biệt:

3x³ - 18x² +27x - 3¹^-m =0

#Mẫu giáo

ha cam

14 tháng 4 2016

giải giúp mình với:

Tìm m để phương trình sau có 3 nghiệm phân biệt:

3x³ - 18x² +27x + 3 - 3^1-m =0

#Mẫu giáo

Pham Trong Bach

25 tháng 8 2018

Cho phương trình m + 2 log 3 2 x + 4 log 3 x + m - 2 = 0 . Tập tất cả các giá trị của tham số thực m để phương trình có hai nghiệm x 1 , x 2 thỏa 0 < x 1 < 1 < x 2 là A. - ∞ ; - 2 B. (-2;2) C. 2 ; + ∞ D. ℝ ...

Đọc tiếp

#Mẫu giáo

Cao Minh Tâm

25 tháng 8 2018

Điều kiện: x > 0

Phương trình trở thành

Khi đó ycbt ⇔ phương trình (*) có hai nghiệm trái dấu

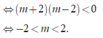
Chọn B.

Đúng(0)

Pham Trong Bach

9 tháng 7 2019

Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình 9 1 - x + 2 ( m - 1 ) 3 1 - x + 1 = 0 có 2 nghiệm phân biệt.

A. m > 1

B. m < -1

C. m < 0

D. -1 < m < 0

#Mẫu giáo

Cao Minh Tâm

9 tháng 7 2019

Đúng(0)

Pham Trong Bach

14 tháng 8 2017

Cho bất phương trình 9 x + ( m - 1 ) 3 x + m > 0 ( 1 ) . Tìm tất cả các giá trị của tham số m để bất phương trình (1) nghiệm đúng ∀ x > 1 A. m ≥ - 3 2 B. m > - 3 2 C. m > 3 + 2 2 D. m ≥ 3 + 2 2 ...

Đọc tiếp

#Mẫu giáo

Cao Minh Tâm

14 tháng 8 2017

Đúng(0)

Pham Trong Bach

20 tháng 6 2019

Cho hàm số y = x 3 - 3 x 2 - m (m là tham số) có đồ thị C m . Tập hợp các giá trị của tham số m để đồ thị C m cắt trục hoành tại ba điểm phân biệt là tập hợp nào sau đây?Tập nghiệm của bất phương trình log 3 x ≤ log 1 3 2 x là nửa khoảng ...

Đọc tiếp

#Mẫu giáo

Cao Minh Tâm

20 tháng 6 2019

Đáp án đúng : C

Đúng(0)

Pham Trong Bach

20 tháng 2 2017

Tìm tất cả các giá trị thực của tham số m để phương trình x 4 − 3 x 2 − m − 1 = 0 có hai nghiệm phân biệt. A. m > − 1 hoặc m = − 13 4 B. m > − 1 C. m ≥ − 1 hoặc m = − 13 4 D. m ≥ − 1 ...

Đọc tiếp

#Mẫu giáo

Cao Minh Tâm

20 tháng 2 2017

Đáp án A

Xét hàm số f x = x 4 − 3 x 2 ,

có f ' x = 4 x 3 − 6 x = 0 ⇔ x = 0 x = ± 6 2 .

Tính các giá trị f 0 = 0 ; f ± 6 2 = − 9 4

=> Đồ thị (C) của hàm số y=f(x) .

Để phương trình f x = m + 1 có 2 nghiệm phân biệt

⇔ m + 1 > 0 m + 1 = − 9 4 ⇔ m > − 1 m = − 13 4

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP