Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Ta có y ' = 3 x 2 + 3 3 a
Hàm sổ có cực trị ⇔ y ' = 0 có 2 nghiệm phân biệt ⇔ a < 0 .
Hàm số là hàm số lẻ nên đồ thị hàm số có tâm đối xứng là gốc tọa độ, do đó đường thẳng nối cực đại và cực tiểu của đồ thị hàm số luôn đi qua gốc tọa độ.
Đáp án C
Phương trình có ba nghiệm phân biệt nếu y c t < m < y c d ⇔ - 2 < m < 2
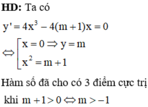
Khi đó điểm cực đại của đồ thị hàm số là A(0;m) và tọa độ 2 điểm cực tiểu là
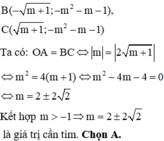
Đáp án A
Ta có: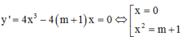 
Hàm số có 3 điểm cực trị khi m > –1
Ba điểm cực trị của đồ thị hàm số là 
; 
Đáp án A
Phương pháp giải:
Tìm tọa độ điểm cực trị của đồ thị hàm số trùng phương và tính diện tích tam giác
Lời giải: TXĐ : D = R
Ta có 
R
Phương trình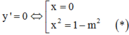 
Hàm số có 3 điểm cực trị ó (*) có 2 nghiệm phân biệt khác 
Khi đó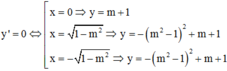 
Gọi 
; 
là ba điểm cực trị. Tam giác ABC cân tại A.
Trung điểm H của BC là 
Và 
Diện tích tam giác ABC là 
Mà 
R suy ra 
Vậy Smax = 1 Dấu bằng xảy ra khi và chỉ khi m = 0
Đáp án là A.
Ta có: y , = 3 x 2 - 6 m x = 0 ⇔ x = 0 x = 2 m
Để đồ thị hàm số có 2 cực trị thì m ≢ 0 suy ra A(0; 4 m 8 ),B(2m;0)
YCBT, ta có m = ± 1 2
Đáp án là A