Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Không dịch được đề
2.
\(-1\le cos2x\le1\Rightarrow1\le y\le3\)
3.
a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b.
\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)
\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)
\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
4.
\(y=\left(tanx-1\right)^2+2\ge2\)
\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)

\(-1\le sin\left(x^2\right)\le1\Rightarrow\)\(0\le\sqrt{1-sin\left(x^2\right)}\le\sqrt{2}\Rightarrow-1\le y\le\sqrt{2}-1\)
\(y_{min}=-1\) khi \(sin\left(x^2\right)=1\Rightarrow x=\pm\sqrt{\dfrac{\pi}{2}+k2\pi}\) (\(k\in N\))
\(y_{max}=\sqrt{2}-1\) khi \(sin\left(x^2\right)=-1\Rightarrow x=\pm\sqrt{-\dfrac{\pi}{2}+k2\pi}\) (\(k\in Z^+\))

Ta có y= 2sin2x +1.
Do - 1 ≤ sin 2 x ≤ 1 ⇒ - 2 ≤ 2 sin 2 x ≤ 2
⇒ - 1 ≤ 2 sin 2 x + 1 ≤ 3 ⇒ - 1 ≤ y ≤ 3
Vậy giá trị lớn nhất của hàm số bằng , giá trị nhỏ nhất bằng .
Chọn C.

Đề là:
\(y=\sqrt{4-3cos^23x}+1\) đúng không nhỉ?
Ta có:
\(0\le cos^23x\le1\Rightarrow1\le\sqrt{4-3cos^23x}\le2\)
\(\Rightarrow2\le y\le3\)
\(y_{min}=2\) khi \(cos^23x=1\)
\(y_{max}=3\) khi \(cos3x=0\)

\(y=2cos^2x-2\sqrt{3}sinx.cosx+1\)
\(=2cos^2x-1-2\sqrt{3}sinx.cosx+2\)
\(=cos2x-\sqrt{3}sin2x+2\)
\(=2\left(\dfrac{1}{2}cos2x-\dfrac{\sqrt{3}}{2}sin2x\right)+2\)
\(=2cos\left(2x+\dfrac{\pi}{3}\right)+2\)
Ta có: \(cos\left(2x+\dfrac{\pi}{3}\right)\in\left[-1;1\right]\)
\(\Rightarrow min=0\Leftrightarrow cos\left(2x+\dfrac{\pi}{3}\right)=-1\Leftrightarrow2x+\dfrac{\pi}{3}=\pi+k2\pi\Leftrightarrow x=\dfrac{\pi}{3}+k\pi\)
\(\Rightarrow max=4\Leftrightarrow cos\left(2x+\dfrac{\pi}{3}\right)=1\Leftrightarrow2x+\dfrac{\pi}{3}=k2\pi\Leftrightarrow x=-\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
\(y=2cos^2x-\sqrt{3}sin2x+1=cos2x-\sqrt{3}sin2x+2\)
\(y=2.cos\left(2x+\dfrac{\pi}{3}\right)+2\)
\(\forall x\in R->-1\le cos\left(2x+\dfrac{\pi}{3}\right)\)
=> \(Min_y=2.\left(-1\right)+2=0\)
Mặt khác, theo Bunhiacopxki:
\(\left(cos2x+\sqrt{3}sin2x\right)^2\le\left(1^2+\sqrt{3}^2\right)\left(cos^22x+sin^22x\right)=4\)
=>\(Max_y=4\)
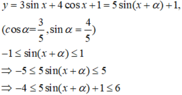
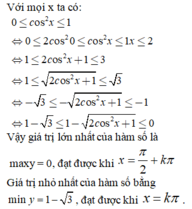
a: ĐKXĐ: 2x<>kpi và cot2x<>-1/căn 3
=>x<>kpi/2 và 2x<>-pi/3+kpi
=>x<>kpi/2 và x<>-pi/6+kpi/2
b: -1<=cos(2x+pi/5)<=1
=>-4<=4cos(2x+pi/5)<=4
=>5<=y<=13
y=5 khi 2x+pi/5=pi+k2pi
=>x=2/5pi+kpi
y=13 khi 2x+pi/5=k2pi
=>x=kpi-pi/10