Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

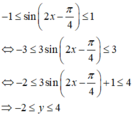
Giá trị lớn nhất và nhỏ nhất của hàm số đã cho là: 4 và - 2
Đáp án A

\(y=5\left[\dfrac{3}{5}sin\left(3x+\dfrac{\pi}{6}\right)+\dfrac{4}{5}cos\left(3x+\dfrac{\pi}{6}\right)\right]\)
\(y=5.sin\left(3x+\dfrac{\pi}{6}+a\right)\) với \(cosa=\dfrac{3}{5}\)
Do \(-1\le sin\left(3x+\dfrac{\pi}{6}+a\right)\le1\)
\(\Rightarrow-5\le y\le5\)

a: ĐKXĐ: 2x<>kpi và cot2x<>-1/căn 3
=>x<>kpi/2 và 2x<>-pi/3+kpi
=>x<>kpi/2 và x<>-pi/6+kpi/2
b: -1<=cos(2x+pi/5)<=1
=>-4<=4cos(2x+pi/5)<=4
=>5<=y<=13
y=5 khi 2x+pi/5=pi+k2pi
=>x=2/5pi+kpi
y=13 khi 2x+pi/5=k2pi
=>x=kpi-pi/10

\(-1\le sin\left(x^2\right)\le1\Rightarrow\)\(0\le\sqrt{1-sin\left(x^2\right)}\le\sqrt{2}\Rightarrow-1\le y\le\sqrt{2}-1\)
\(y_{min}=-1\) khi \(sin\left(x^2\right)=1\Rightarrow x=\pm\sqrt{\dfrac{\pi}{2}+k2\pi}\) (\(k\in N\))
\(y_{max}=\sqrt{2}-1\) khi \(sin\left(x^2\right)=-1\Rightarrow x=\pm\sqrt{-\dfrac{\pi}{2}+k2\pi}\) (\(k\in Z^+\))


0 ≤ |sinx| ≤ ln n - 2 ≤ -2|sinx| ≤ 0
Vậy giá trị lớn nhất của y = 3 - 2|sin x| là 3, đạt được khi sin x = 0; giá trị nhỏ nhất của y là 1, đạt được khi sinx = 1 hoặc sinx = -1

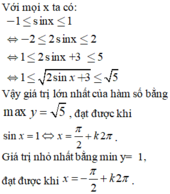
Đáp án C