Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
B P T ⇔ 3 3 x 2 − 10 10 x + 3 ≤ 0 ⇔ 1 3 ≤ 3 x ≤ 3 ⇔ − 1 ≤ x ≤ 1 ⇒ ⇒ T = 2.

Đáp án C
Vì x = 1 là một nghiệm của bất phương trình
⇒ log m 4 ≤ log m 2 ⇔ log m 2 ≤ 0 ⇔ m ∈ 0 ; 1 .
Khi đó, bất phương trình
log m 2 x 2 + x + 3 ≤ log m 3 x 2 − x ⇔ 3 x 2 − x > 0 2 x 2 + x + 3 ≥ 3 x 2 − x ⇔ − 1 ≤ x < 0 1 3 < x ≤ 3 .

Bất phương trình tương đương với 3 . 3 2 x - 10 . 3 x + 3 ≤ 0
Đặt t = 3 x > 0 Bất phương trình trở thành 3 t 2 - 10 t + 3 ≤ 0 ⇔ 1 3 ≤ t ≤ 3 .
Với 1 3 ≤ t ≤ 3 , ta được 1 3 ≤ 3 x ≤ 3 ⇔ - 1 ≤ x ≤ 1
Do đó tập nghiệm của bất phương trình là S = [ -1;1 ]
Vậy b - a = 2
Đáp án C

Đáp án C
Điều kiện: x < 1 2 . Bất phương trình tương đương
1 − 2 x ≤ 8 ⇔ x ≥ − 7 2 ⇒ S = − 7 2 ; 1 2 .

Đáp án A.
Phương pháp:
Xét hàm số y = log a x :
*Nếu 0 < a < 1 : Hàm số nghịch biến trên 0 ; + ∞
*Nếu a > 1 : Hàm số đồng biến trên 0 ; + ∞ .
Cách giải:
log 1 2 x − 3 ≥ log 1 2 4 ⇔ x − 3 > 0 x − 3 ≤ 4 ⇔ x > 3 x ≤ 7 ⇔ 3 < x ≤ 7


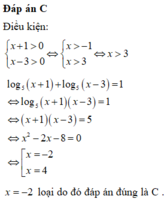
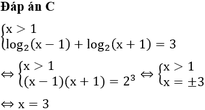
Bất phương trình tương đương với
3 x x 2 - 9 ≤ 0 ⇔ x 2 - 9 ≤ 0 ⇔ - 3 ≤ x ≤ 3
Vậy S = - 3 ; 3
Đáp án A