MT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QT
1
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Tập xác định của hàm số là \(D = \mathbb{R}\)
Vì \(-1\le sinx\le1\)
\( \Rightarrow \) Tập giá trị của hàm số \(y = 2\sin x\) là \(T = \left[ { - 2;2} \right]\).
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Tập xác định của hàm số là \(D = \mathbb{R}\)
Vì \( - 1 \le \sin \left( {x - \frac{\pi }{4}} \right) \le 1 \Rightarrow - 2 \le 2\sin \left( {x - \frac{\pi }{4}} \right) \le 2\; \Rightarrow - 2 - 1 \le 2\sin \left( {x - \frac{\pi }{4}} \right) - 1 \le 2 - 1\)
\( \Rightarrow - 3 \le 2\sin \left( {x - \frac{\pi }{4}} \right) - 1 \le 1\)
Vây tập giá trị của hàm số \(y = 2\sin \left( {x - \frac{\pi }{4}} \right) - 1\) là \(T = \left[ { - 3;1} \right]\).
b) Tập xác định của hàm số là \(D = \mathbb{R}\)
Vì \( - 1 \le \cos x \le 1 \Rightarrow 0 \le 1 + \cos x \le 2 \Rightarrow 0 \le \sqrt {1 + \cos x} \le \sqrt 2 \;\; \Rightarrow - 2 \le \sqrt {1 + \cos x} - 2 \le \sqrt 2 - 2\)
Vậy tập giá trị của hàm số \(y = \sqrt {1 + \cos x} - 2\) là \(T = \left[ { - 2;\sqrt 2 - 2} \right]\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Tập xác định của hàm số là \(D = \mathbb{R}\)
Vì \( - 1 \le \cos \left( {2x - \frac{\pi }{3}} \right) \le 1 \Leftrightarrow - 2 \le 2{\rm{cos\;}}\left( {2x - \frac{\pi }{3}} \right) \le 2\;\; \Leftrightarrow - 3 \le 2\cos \left( {2x - \frac{\pi }{3}} \right) - 1 < 1\)
\( \Rightarrow \) Tập giá trị của hàm số \(y = 2\cos \left( {2x - \frac{\pi }{3}} \right) - 1\) là \(T = \left[ { - 3;1} \right]\).
b) Tập xác định của hàm số là \(D = \mathbb{R}\)
Vì \( - 1 \le \sin x \le 1,\;\; - 1 \le \cos \alpha \le 1\;\; \Leftrightarrow - 2 \le \sin x + \cos x \le 2\)
\( \Rightarrow \) Tập giá trị của hàm số \(y = \sin x + \cos x\) là \(T = \left[ { - 2;2} \right]\).
NH
1
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 7 2021
Đặt \(sinx=t\Rightarrow t\in\left[-\dfrac{1}{2};1\right]\)
\(y=f\left(t\right)=2t^2+t+4\)
Xét hàm \(f\left(t\right)=2t^2+t+4\) trên \(\left[-\dfrac{1}{2};1\right]\)
\(-\dfrac{b}{2a}=-\dfrac{1}{4}\in\left[-\dfrac{1}{2};1\right]\)
\(f\left(-\dfrac{1}{2}\right)=4\) ; \(f\left(-\dfrac{1}{4}\right)=\dfrac{31}{8}\); \(f\left(1\right)=7\)
\(y_{max}=7\) khi \(t=1\) hay \(x=\dfrac{\pi}{2}\)
\(y_{min}=\dfrac{31}{8}\) khi \(sinx=-\dfrac{1}{4}\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
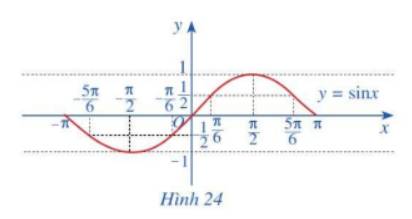
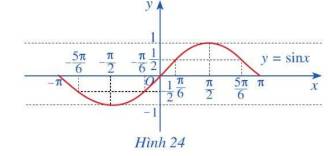
a)
x | \( - \pi \) | \( - \frac{{5\pi }}{6}\) | \( - \frac{\pi }{2}\) | \( - \frac{\pi }{6}\) | 0 | \(\frac{\pi }{6}\) | \(\frac{\pi }{2}\) | \(\frac{{5\pi }}{6}\) | \(\pi \) |
\(y = \sin x\) | 0 | \( - \frac{1}{2}\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 |
b) Trong mặt phẳng Oxy, hãy biểu diễn các điểm \(\left( {x;y} \right)\) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\sin x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) với nối lại ta được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\)(Hình 24).
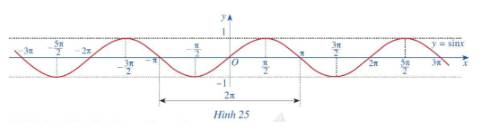
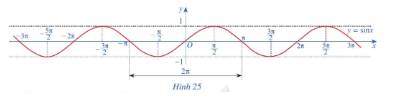
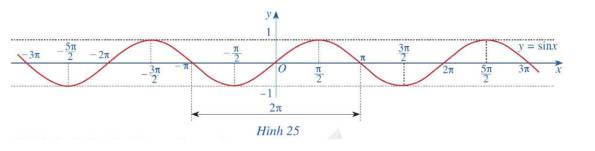
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \sin x\)trên R được biểu diễn ở Hình 25.
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Tập giá trị của hàm số\(y = \sin x\) là \(\left[ { - 1;1} \right]\)
b) Đồ thị hàm số \(y = \sin x\) nhận O là tâm đối xứng.
Như vậy hàm số \(y = \sin x\) là hàm số lẻ.
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\)
Như vậy, hàm số \(y = \sin x\) có tuần hoàn .
d) Hàm số \(y = \sin x\) đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\) với \(k \in Z\)
12 tháng 9 2021
1, \(y=2-sin\left(\dfrac{3x}{2}+x\right).cos\left(x+\dfrac{\pi}{2}\right)\)
\(y=2-\left(-cosx\right).\left(-sinx\right)\)
y = 2 - sinx.cosx
y = \(2-\dfrac{1}{2}sin2x\)
Max = 2 + \(\dfrac{1}{2}\) = 2,5
Min = \(2-\dfrac{1}{2}\) = 1,5
2, y = \(\sqrt{5-\dfrac{1}{2}sin^22x}\)
Min = \(\sqrt{5-\dfrac{1}{2}}=\dfrac{3\sqrt{2}}{2}\)
Max = \(\sqrt{5}\)
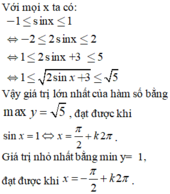
\(Vì-1\le\sin x\le1\)
\(\Rightarrow-2\le2\sin x\le2\)
\(\Rightarrow3\le5+2\sin x\le7\)
\(\Rightarrow3\le y\le7\)
\(Vậy\) \(y_{max}=7\)
\(y_{min}=3\)