PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MH
5 tháng 2 2022
Tham khảo:
Ta có: \(R=\dfrac{abc}{4S};r=\dfrac{S}{p}\)
Vì tam giác ABC vuông cân tại A nên \(b=c\) và \(a=\sqrt{b^2+c^2}=b\sqrt{2}\)
Xét tỉ số:
\(\dfrac{R}{r}=\dfrac{abc.p}{4S^2}=\dfrac{abc.\dfrac{a+b+c}{2}}{4.\dfrac{1}{4}.\left(b.c\right)^2}=\dfrac{a\left(a+2b\right)}{2b^2}=\dfrac{2b^2\left(1+\sqrt{2}\right)}{2b^2}=1+\sqrt{2}\)
13 tháng 1 2022
a: \(\overrightarrow{AB}=\left(-3;4\right)\)
\(\overrightarrow{AC}=\left(8;6\right)\)
Vì \(\overrightarrow{AB}\cdot\overrightarrow{AC}=0\) nên ΔABC vuông tại A
c: Tọa độ trọng tâm G là:
\(\left\{{}\begin{matrix}x_G=\dfrac{1-2+9}{3}=\dfrac{8}{3}\\y_G=\dfrac{2+6+8}{3}=\dfrac{16}{3}\end{matrix}\right.\)
CM
31 tháng 10 2018
Ta có: A B 2 + A C 2 = 3 2 + 4 2 = 5 2 ⇒ A B 2 + A C 2 = B C 2
⇒ ∆ABC vuông tại A.
Diện tích tam giác ABC là:
S ∆ A B C = 1 2 A B . A C = 1 2 . 3 . 4 = 6 .
Nửa chu vi của tam giác là p = 1 / 2 ( 3 + 4 + 5 ) = 6 .
Bán kính đường tròn nội tiếp của tam giác ABC là:
r = S p = 6 6 = 1 . Chọn D.
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1 2021
\(\overrightarrow{AB}=\left(4;0\right)=4\left(1;0\right)\) ; \(\overrightarrow{AC}=\left(3;3\right)=3\left(1;1\right)\)
Gọi M là trung điểm AB, N là trung điểm AC \(\Rightarrow\left\{{}\begin{matrix}M\left(1;1\right)\\N\left(\dfrac{1}{2};\dfrac{5}{2}\right)\end{matrix}\right.\)
Phương trình trung trực AB:
\(1\left(x-1\right)+0\left(y-1\right)=0\Leftrightarrow x-1=0\)
Phương trình trung trực AC:
\(1\left(x-\dfrac{1}{2}\right)+1\left(y-\dfrac{5}{2}\right)=0\Leftrightarrow x+y-3=0\)
Tọa độ I là nghiệm:
\(\left\{{}\begin{matrix}x-1=0\\x+y-3=0\end{matrix}\right.\) \(\Rightarrow I\left(1;2\right)\)
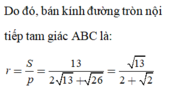
Dễ dàng viết được phương trình đoạn AB là :
4x−3y−65=04x−3y−65=0
và phương trình đoạn AC là:
9x+12y−15=09x+12y−15=0
Phương trình đường phân giác góc A là:
|4x−3y−65|5=|9x+12y−15|15|4x−3y−65|5=|9x+12y−15|15
Từ đó ta rút ra 2 phương trình đường phân giác :
3x−21y−180=03x−21y−180=0 (Δ1)(Δ1)
Hoặc 21x+3y−210=021x+3y−210=0 (Δ2)(Δ2)
Xét (Δ1)(Δ1) : f(x,y)=3x−21y−180f(x,y)=3x−21y−180
f(xB,yB)=−323f(xB,yB)=−323
f(xC,yC)=−255f(xC,yC)=−255
=>=> f(xB,yB).f(xC,yC)≥0f(xB,yB).f(xC,yC)≥0
=>=> B, C nằm cùng phía với đường thẳng (Δ1)(Δ1)
=>=> phương trình đường phân giác trong góc A là : 21x+3y−210=021x+3y−210=0 (Δ2)(Δ2)
Hoàn toàn tương tự ta có phương trình đường phân giác trong góc B là: 27x−39y−270=027x−39y−270=0 (Δ3)(Δ3)
Gọi I là tâm đường tròn nội tiếp ΔABCΔABC hay I là giao điểm 2 đường phân giác trong (Δ2)(Δ2) và (Δ3)(Δ3)
Từ đó tọa độ của I là nghiệm hệ pt:
{21x+3y−210=027x−39y−270=0{21x+3y−210=027x−39y−270=0
<=><=> {x=10y=0{x=10y=0
vậy tâm I có tọa độ là (10;0)(10;0)
từ tâm I dùng công thức khoảng cách đến các cạnh tam giác ABC rồi suy ra bán kính bằng 5 (đvđd)
xong nhé