Tìm số x không âm, biết: a ) √ x

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

11 tháng 6 2019

Tìm số x không âm, biết:

a ) √ x > 1 ; b ) √ x < 3 .

#Toán lớp 9

Cao Minh Tâm

11 tháng 6 2019

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Trang Ngọc

30 tháng 10 2021 - olm

Tìm số x không âm, biết a) √x (√x-1)?= 0 b) (√x-2) (√x+3) = 0 c) (√x +1) (√x+2) = 0

#Toán lớp 9

Lê Song Phương

31 tháng 10 2021

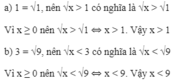
a) \(\sqrt{x}\left(\sqrt{x}-1\right)=0\Leftrightarrow\orbr{\begin{cases}\sqrt{x}=0\\\sqrt{x}-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=1\end{cases}}\)

b) \(\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)=0\Leftrightarrow\orbr{\begin{cases}\sqrt{x}-2=0\\\sqrt{x}+3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=4\\\sqrt{x}=-3\left(vôlí\right)\end{cases}}\)

c) \(\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)=0\Leftrightarrow\orbr{\begin{cases}\sqrt{x}+1=0\\\sqrt{x}+3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}\sqrt{x}=-1\left(vôlí\right)\\\sqrt{x}=-3\left(vôlí\right)\end{cases}}\)

Đúng(0)

NT Ánh

9 tháng 8 2016

tìm số x không âm ,biết:

a) \(\sqrt{x}\)>1
b) \(\sqrt{x}\)<3

#Toán lớp 9

Trần Việt Linh

9 tháng 8 2016

a) \(\sqrt{x}>1\Leftrightarrow x>1\)

b) \(\sqrt{x}< 3\Leftrightarrow x< 9\)

Vì x không âm nên x={0;1;2;3;4;5;6;7;8}

Đúng(0)

Lightning Farron

9 tháng 8 2016

a)\(\sqrt{x}>1\Leftrightarrow\sqrt{x^2}>1^2\Leftrightarrow x>1\)

b)\(\sqrt{x}< 3\Leftrightarrow\sqrt{x^2}< 3^2\Leftrightarrow x< 9\)

Đúng(0)

Pham Trong Bach

8 tháng 7 2018

Tìm số x không âm, biết:

a) √ x = 15 ; b) 2 √ x = 14

c) √ x < √ 2 ; d) √ 2 x < 4

#Toán lớp 9

Cao Minh Tâm

8 tháng 7 2018

Lưu ý: Vì x không âm (x ≥ 0) nên các căn thức trong bài đều xác định.

a) √ x = 15

Vì x ≥ 0 nên bình phương hai vế ta được:

x = 15 2 ⇔ x = 225

Vậy x = 225

b) 2 √ x = 14 ⇔ √ x = 7

Vì x ≥ 0 nên bình phương hai vế ta được:

x = 7 2 ⇔ x = 49 V ậ y x = 49

c) √x < √2

Vì x ≥ 0 nên bình phương hai vế ta được: x < 2

Vậy 0 ≤ x < 2

d) 2 x < 4

Vì x ≥ 0 nên bình phương hai vế ta được:

2x < 16 ⇔ x < 8

Vậy 0 ≤ x < 8

Đúng(0)

Phạm lệ thu

16 tháng 8 2018 - olm

1. Tìm số x không âm,biết :

a) 2√x = 14

b) √x < √2

c) √2x < 4

#Toán lớp 9

nguyễn thị thanh thùy

16 tháng 8 2018

\(2\sqrt{x}=14\Rightarrow\sqrt{x}=7\) \(\Rightarrow x=49\)

\(\sqrt{x}< \sqrt{2}\Rightarrow x< 2\) Mà x không âm \(\Rightarrow x\in\left(0;1\right)\)

\(\sqrt{2x}< 4\Rightarrow2x< 16\) \(\Rightarrow x< 8\) mà x không âm \(\Rightarrow x\in\left(0;1;2;3;4;5;6;7\right)\)

Đúng(0)

Pham Trong Bach

30 tháng 10 2018

Tìm số x không âm, biết: √x < 3.

#Toán lớp 9

Cao Minh Tâm

30 tháng 10 2018

3 = √9, nên √x < 3 có nghĩa là √x < √9

Vì x ≥ 0 nên √x < √9 ⇔ x < 9. Vậy x < 9

Đúng(0)

Pham Trong Bach

10 tháng 6 2018

Tìm số x không âm, biết:

√x > 1

#Toán lớp 9

Cao Minh Tâm

10 tháng 6 2018

1 = √1, nên √x > 1 có nghĩa là √x > √1

Vì x ≥ 0 nên √x > √1 ⇔ x > 1. Vậy x > 1

Đúng(0)

Trà Nguyễn

30 tháng 8 2021

Tìm số x không âm , biết

a, √x < √2;

#Toán lớp 9

Lê Đức Huy

30 tháng 8 2021

Xin in4 đi bạn

Đúng(0)

Lê Đức Huy

30 tháng 8 2021

Rồi mình chỉ cho

Đúng(1)

NT Ánh

9 tháng 8 2016

Tìm số x không âm,biết:

a) \(\sqrt{x}\)>2

b)\(\sqrt{x}\)<1

#Toán lớp 9

Lightning Farron

9 tháng 8 2016

a)\(\sqrt{x}>2\Leftrightarrow\sqrt{x^2}>2^2\Leftrightarrow x>4\)

\(\sqrt{x}< 1\Leftrightarrow\sqrt{x^2}< 1^2\Leftrightarrow x< 1\)

Đúng(0)

Nguyễn Nho Bảo Trí

6 tháng 6 2021

Tìm số x không âm , biết :

a) \(\sqrt{x}\)= 15

b) \(2\sqrt{x}\)= 14

c) 2\(2\sqrt{x}\) < 4

#Toán lớp 9

Nguyễn Nho Bảo Trí

6 tháng 6 2021

Giúp mình với

Đúng(0)

Nguyễn Thị Ngọc Thơ

6 tháng 6 2021

a, x = 225

b, x = 49

c, x < 4

Đúng(1)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP